Carrier concentration in intrinsic semiconductors

CARRIER CONCENTRATION IN INTRINSIC SEMICONDUCTORS

Definition

The number of electrons in conduction band per unit volume of the material is called as electron concentration (n).

Similarly the number of holes in valence band per unit volume of the material is called hole concentration (p).

In general, the number of charge carriers per unit volume of the material is called carrier concentration. It is also known as density of charge carriers.

Density of Electrons in Conduction Band (Derivation)

The number of electrons per unit volume in conduction band for energy between E and E+ dE is given by

dn = Z (E) F (E) dE    ...(1)

where Z (E) dE - Density of states in energy between E and E+ dE

F (E) - Probability of electron occupancy.

Number of electrons in conduction band for the entire range is calculated by integrating eqn (1) between energy Ec and + ∞.

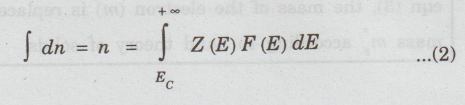
Ec is energy corresponding to the bottom most level and +∞ is energy corresponding to the upper most level in conduction band. (Fig 3.5).

Density of states in conduction band between the energy range E and E+ dE is given by

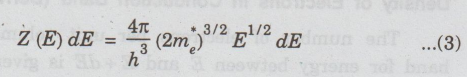
The bottom edge of the conduction band (E_C) denotes the potential energy of an electron at rest. Therefore, (E - E_C) is the kinetic energy of conduction electron at higher energy levels.

Thus, in eqn (3), E is replaced as (E - E_C)

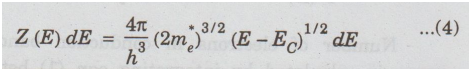
The electrons in conduction band are not totally free. They move in a periodic potential of the crystal lattice. Therefore, in eqn (3), the mass of the electron (m) is replaced by its effective mass m^*_e according to band theory of solids.

The probability of electron occupation is given by Fermi distribution function

F (E) = 1 / 1 + e^(E-EF)/kT  ...(5)

Substituting eqns (4) and (5) in (2), we get

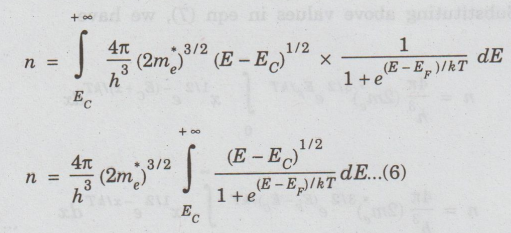
Since kT is very small and (E - E_F) is greater than kT, (E – E_F)^/kT is very large compared to '1' Hence, '1' from the denominator of eqn (6) is neglected.

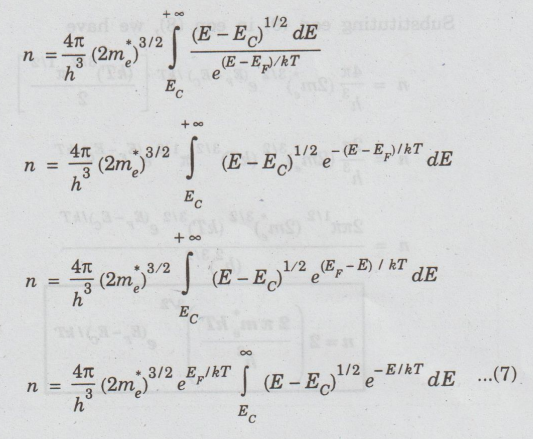
To evaluate above integral in eqn (7), let us assume

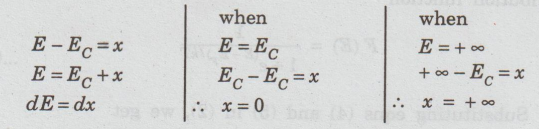
Substituting above values in eqn (7), we have

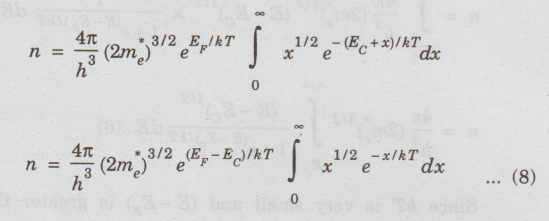
Using the gamma function, it is shown that

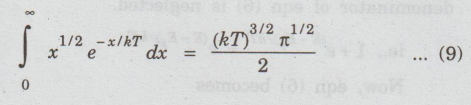
Substituting eqn (9) in eqn (8), we have

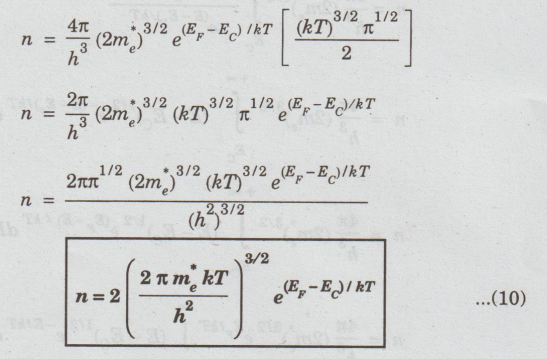
Equation (10) is the expression for concentration of electrons in the conduction band of intrinsic semiconductor.

Density of holes in Valence Band of Intrinsic Semiconductor (Derivation)

We know that if an electron is transferred from valence band to conduction band, a hole is created in valence band.

Let dp be the number of holes per unit volume in valence band between the energy E and E + dE.

dp = Z (E) (1-F (E)) dE        ...(1)

where Z (E) dE → Density of states in the energy range E and E + dE.

Since F (E) is the probability of electron occupation 1-F (E) is the probability of an unoccupied electron state, i.e., probability of presence of hole,

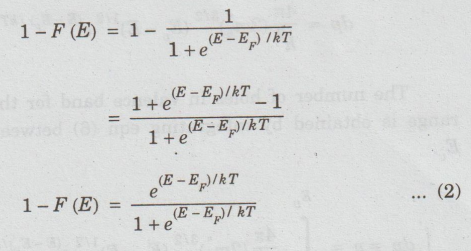
Since E is very small when compared to E in valence band, (E-E) is a negative quantity. Therefore, e ^{(E - EF)/kT} is very small and it is neglected in the denominator term of eqn (2).

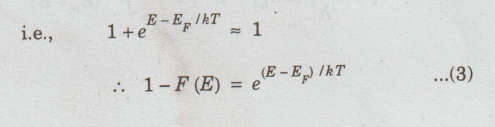
Density of states in valence band,

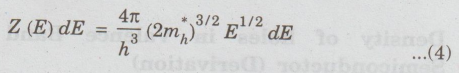
Here, m is the effective mass of the hole in valence band.

E_U’ top of energy level in valence band is the potential energy of a hole at rest. Hence, (E_U - E) is the kinetic energy of the hole at level below E. So the term E in eqn (4) is replaced as (E_U - E).

Z (E) dE = 4π / h³ (2m^*_h)3/2 (E_U – E)^1/2 dE  ...(5)

Substituting eqns (3) and (5) in (1), we get

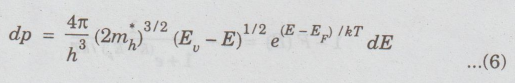
The number of holes in valence band for the entire energy range is obtained by integrating eqn (6) between limits - ∞ to E_U.

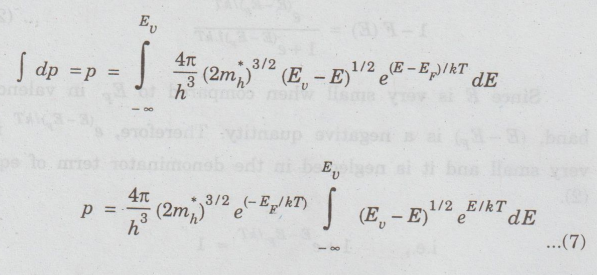
To evaluate the integral in eqn (7), let us assume,

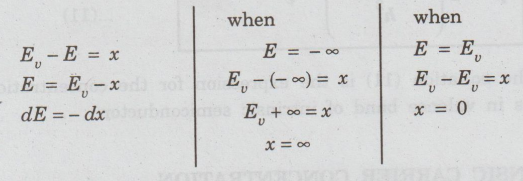
Substituting these values in eqn (7), we have

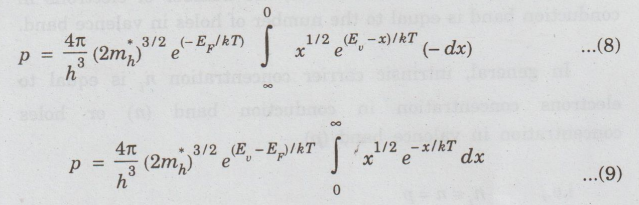
 [-ve sign is omitted by interchanging the limits]

Using the gamma function, it is shown that

Substituting eqn (10) in eqn (9), we have

The equation (11) is the expression for the concentration of holes in valence band of intrinsic semiconductor.