Conductivity of metallic nanowires

CONDUCTIVITY OF METALLIC NANOWIRES

Let us study what happens when wire length L becomes extremely small relative to the mean free path and the influence of wire cross-section size on conductivity of metallic nanowires.

Consider a circular cross-section wire which has radius a and length L. Assume that L is very large compared to the mean free path.

For example, assuming a copper (σ = 5.9 × 10⁷ S/m) wire having radius ɑ = 10 mm, R = 5.395 × 10^-5 ohms/m. However if ɑ = 10 μ m, R = 53.95 ohms/m amounting to 1 ohm in only 1.85 cm. If ɑ = 10 nm, the resistance is huge, R = 5.395 × 10⁷ohms/m.

It is important to note that for wires having radius values in the order of the mean free path or less the conductivity value is changed from the case of a bulk material.

For example, copper has a mean free path of approximately 40 nm, and in this range, radius-dependent effects are usually manifest.

In fact, we may consider that radius dependent effects may occur even when the radius is approximately double this value, in the order of 80 - 100 nm.

In the 1 - 20 nm radius range, the conductivity of the wire certainly will differ appreciably from the bulk value, and generally the conductivity significantly decreases as a is reduced.

This is due to several effects, such as scattering from the wire's surface, from grain boundaries defects etc.,

Thus, we can use the bulk value of conductivity for many good conductors when the radius value is above approximately a = 80 - 100 nm.

Below this point, down to radius values of perhaps 5-10 nm (but above metallic quantum wire dimensions), we may expect to need to use a size dependent value of conductivity, perhaps based on measurement.

A relatively simple approximate formula for the resistivity (p) of rectangular cross-section wires is

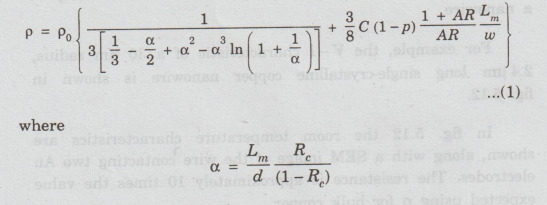
where P₀ - bulk resistivity

w - wire width

AR - Physics for Electrical Engineering

AR aspect ratio (wire height divided by wire width),

d - average grain size (for relatively narrow wires this can be taken as the wire width),

p - specularity parameter (relating to reflection from the wire surface),

R_e - grain boundary reflectivity coefficient

C - a constant (taken to be 1.2 in this model).

The first term is related to grain-boundary scattering and the second term wire-surface scattering.

Both p and R_c can take values between 0 and 1, and typical values determined by fitting equation (1) to experimental results are p = 0.3-0.5 and R_c = 0.2 - 0.3.

For example, using p = 0.50 and R_e = 0.27 we have σ = 1.22 × 10⁷ S/m for a 10 × 10 nm² copper wire (down from 5.9 × 10⁷ S/m for the bulk value).

This model may work down to wire cross-sectional dimensions in the order of 5-10 nanometres.

However, as complicated as surface and grain-boundary scattering are other factors also determine the conductivity of a nanowire.

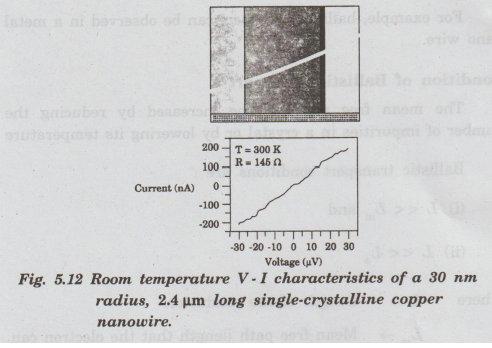
For example, the V-I characteristic of a 30 nm radius, 2.4 μm long single-crystalline copper nanowire is shown in fig. 5.12.

In fig. 5.12 the room temperature characteristics are shown, along with a SEM image of the wire contacting two Au electrodes. The resistance is approximately 10 times the value expected using σ for bulk copper.