Crystal Oscillator

CRYSTAL OSCILLATOR

The frequency of LC and RC oscillators may change with time, temperature changes, etc. Hence the frequency of oscillations does not remain constant. Therefore the LC oscillators are not suitable high frequency stability requirement.

Some naturally available crystals (such as, quartz) have the property that their resonant frequencies are constant. Hence a crystal is used as the frequency determining element in an oscillator for high frequency stability. Such oscillator is called a crystal oscillator.

When a piezoelectric proper alternating potential, vibrates mechanically. The amplitude of these mechanical oscillations maximum when the frequency of the applied alternating voltage is equal to the natural frequency of the crystal.

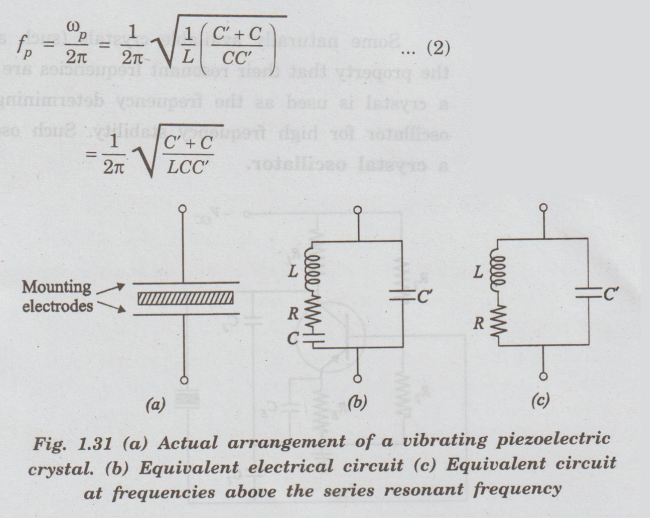
The equivalent electrical circuit of a vibrating piezoelectric crystal is represented by a series resonant LCR circuit shunted by a capacitance C', as shown in fig.1.31(b). The inductance L is the electrical equivalent of the mass of the crystal. The capacitance C is the electrical equivalent of the mechanical compliance, and the resistance R represents the electrical equivalent of the mechanical friction.

 The capacitance C' represents the electrostatic capacitance between the mounting electrodes when the crystal is not vibrating. C' also induces any capacitance due to the crystal holder. The values of the L, C, R and C' depends upon the crystal cut, its and the nature of the vibrations involved.

The series resonance frequency is given by

f_s = ω_s / 2л 1/ 2π √LC... (1)

where f_s is called the series resonant frequency. At this frequency the impedance of the series arm is resistive and has a low value equal to R.

or

The parallel resonance frequency f_p is given by

The ratio of C'/C is usually several hundred. Hence Eq. (2) can be written

f_p= 1 / 2π √ LC....(3)

Thus the series resonant frequency f_s is very close to the parallel resonant frequency f_p. At f_p the crystal offers a very high impedance to the internal circuit.

The resonant frequencies of a crystal are inversely proportional to the thickness of the cut and are different cuts. In general crystal can be used in the frequency range from about 15 kHz to 10 MHz.

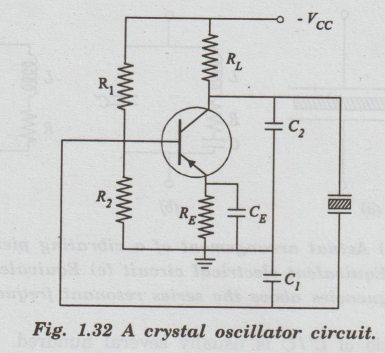
A crystal oscillator circuit is shown in fig.1.32. In this circuit the crystal operates in its parallel-resonant mode.

Since the resistance R of a crystal is very small, the Q (Quality factor) of the crystal is very high.

Hence the frequency stability of the crystal oscillator is also very high.

Advantages of crystal oscillators

1.The Q factor of a crystal is very high of the order 10⁶ compared to that of an LC circuit and hence, the frequency of crystal is highly stable.

Thus f_r / Q  = bandwidth virtually becomes zero. The circuit frequency depends upon the crystal resonance frequency alone.

2. By changing the crystal different frequencies can be achieved.

3. The frequency drift can be made less than 1 part in 10⁶.

4. The rate of change of phase shift θ with angular frequency ω (d θ/d ω) is large, frequency change is very small even if the phase shift of the circuit changes.

5. Crystal oscillator does not need a separat tuned circuit. oals at

Disadvantages

 1.As the crystal has got a very large Q; the crystal vibrates only at resonant frequency and does not vibrate at the other frequencies.

2. If excessive power is applied, the oscillator waveform basin will be distorted.

3.Overheating causes frequency drift and the crystal being fragile is likely to fail.

4. A crystal oscillator is used in low power circuits.

Application and uses

• Crystal oscillators are used in frequency synthesisers, which have revolutionised the frequency scene in communication equipment. It is now possible to have complete systems economically.

• They are used to generate a chromatic sub-carrier or color sub-carrier in TV receivers.

•They got wide applications in microprocessors, microcontrollers, embedded systems, electronics clocks and watches, frequency and time standards, generates in radio and computer-clock pulse communication equipment.