Dielectric Loss

DIELECTRIC LOSS

When a dielectric is applied with AC voltage, the electrical energy is absorbed by the dielectric and certain quantity of electrical energy is dissipated in the form of heat energy.

This dissipation of electrical energy is known as dielectric loss.

Dielectric loss can occur in both direct and alternating voltages. It is less in direct voltage than that of alternating voltage.

Expression for dielectric loss (or loss tangent)

When an AC voltage is applied to a perfect dielectric like vacuum or purified gas, it does not absorb electrical energy and there is no loss of electrical energy [fig. 1.12 (a)].

Polarisation of the dielectric is in phase with the voltage. In such a case, the charging current leads the applied voltage by an angle of 90° as shown in fig 1.12 (b).

We know that power loss,

P_L = VI cos θ

When θ = 90°, P_L=V I cos90°

P_L= 0

[ cos 90° = 0]

This means that there is no power loss in the perfect dielectric.

However, a practical dielectric has always some loss of electrical energy. In this case, the leakage current does not lead the applied voltage exactly by 90°.

The phase angle (θ) is always less than 90° as shown in fig. 1.12(c).

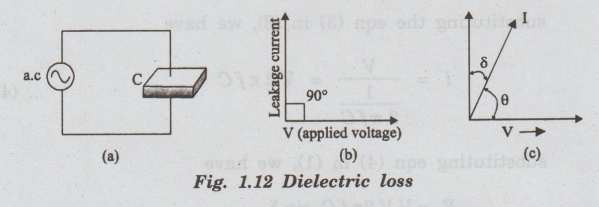
The current leads the voltage by (90 – δ ). This shows that there is some loss in electrical energy. δ is called dielectric loss angle. This loss angle is a measure of the power dissipated in each cycle.

The power loss in a dielectric having a capacitance C for applied voltage V of frequency f is given by

PL=VI cos θ

Since θ = 90- δ, we have

P_L = VI cos (90° - δ) .... (1)

P_L = VI sin δ [cos(90° - δ) = sin δ]

We know that V = IR or I = V / R

Similarly, for capacitor if the capacitive reactance is X_e, we can write

I = V / X_c... (2)

Further, X_c depends on frequency of applied a.c voltage and capacitance. It is given by

X_c = 1 / 2 л f С ...(3)

substituting the eqn (3) in (2), we have

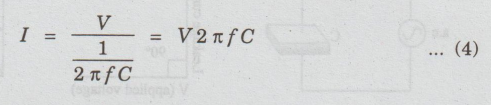
substituting eqn (4) in (1), we have

P_L=VV 2π fC sin δ

Р_L = 2π f C V² sin δ

In most of the dielectrics, the angle δ is very small.

sin δ = tan δ

Dielectric power loss P_L = 2n fC V²tan δ ... (6)

It is noted that the power loss depends on tan 8 as long as other factors like voltage, frequency and capacitance are constant.

 tan δ  is called the power factor of the dielectric.

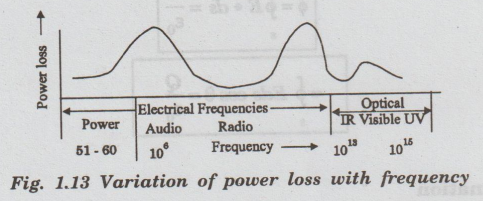
Variation of power loss with frequency

The power loss changes with frequency. Its value is high in the electrical frequency and low in the optical frequency (fig. 1.13).

Factors affecting dielectric loss

Dielectric loss may increase due to the following factors.

• high frequency of the applied voltage

• high value of the applied voltage

• presence of humidity

• temperature rise

Note: Dielectric loss is an engineering problem involving heat generation and heat dissipation. It plays a dominant role in high voltage applications.