Electronic Polarisation

ELECTRONIC POLARISATION

Electronic polarisation is due to the displacement of positively - charged nucleus and negatively – charged electrons of an atom in opposite directions on the application of an electrical field. This induces dipole moment in the dielectric.

Dipole moment (μ) is proportional to the electric field strength (E).

i.e., μ ∝ Ε

μ = α_e Ε

where α_e is proportionality constant and it is known as electronic polarisability.

Calculation of Electronic polarisability (α_e)

(i) Without electric field

Consider an atom of a dielectric material of nuclear charge + Ze at the centre (point change), where Z is the atomic number. The electrons of charge (- Ze) are distributed uniformly throughout the atom (sphere) of radius R as shown in fig. 1.4.

The centres of electron cloud and positive nucleus are at the same point and hence there is no dipole moment.

Negative charge density of atom is given by

ρ = Total negative charge / Volume of the atom = - Z e / 4/3 πR³

ρ = -3/4  Ze / πR³ .........(1)

 (ii) With electric field

When the atom of the dielectric is placed in an electrical field of strength E, two phenomena occur

(a) Lorentz force (due to electrical field) tends to move the nucleus and electron cloud of that atom from their equilibrium positions.

The positive nucleus moves towards the field direction and the electron cloud moves in opposite direction of the field as shown in fig.1.5.

(b) After separation, an attractive Coulomb force arises between the nucleus and the electron cloud which tends to maintain the original equilibrium position.

When these two forces are equal and opposite, there is a new equilibrium between the nucleus and electron cloud of the atom.

The electron cloud and the nucleus are separated by a distance 'x'. It results in formation of electrical dipole in the atom.

Lorentz force between nucleus and electron F_L = Charge × electrical field

= ZeE... (2)

Coulomb attractive force (F_C) between nucleus and electron cloud being separated at a distance x,

F_C = Q_p Q_e / 4πε₀ x² ................(3)

= Nuclear plaib Charge (Ze) × Total negative charges enclosed in the sphere of radius x / 4πε₀x²

Total negative charges enclosed in the sphere of radius x = Charge density (ρ) × Volume of the sphere of radius x

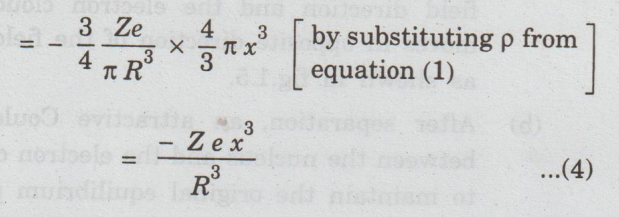
Total positive charge of atom present in the sphere of radius x,

Q_p = + Ze (being a point charge)

Substituting the equation (4) in (3), we have

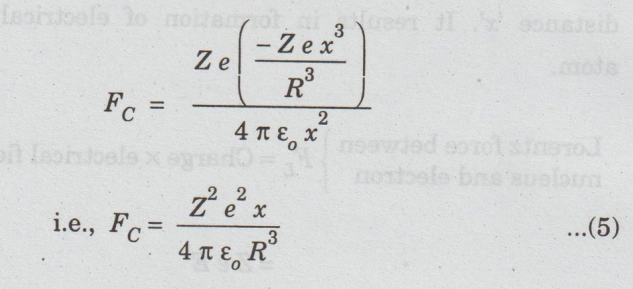
At equilibrium, Coulomb force and Lorentz force must be equal and opposite.

i.e., F_L=- - F_C

Substituting for F_L and F_C from equation (2) and (5), we have

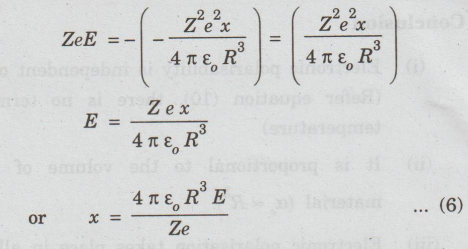
Due to the application of electrical field on the atom, the charge centres are displaced from their equilibrium position and hence the atom gains some dipole moment.

From the definition of dipole moment, induced dipole moment (μ_ind) is given by

μ_ind = Magnitude of charge × Displacement

i.e., μ_ind = Z e x........(7)

Substituting equation (6) in (7), we have

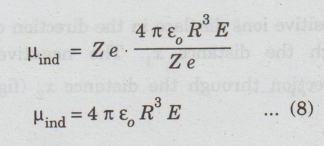
But, the induced dipole moment

in terms of polarisability is given by,

μ_ind = ɑ_e E.............(9)

where ɑ_e is called as electronic polarisability.

On comparing the equations (8) and (9), we have

α_e = 4 πε₀ R³.................(10)

Conclusion

(i) Electronic polarisability is independent of temperature. (Refer equation (10), there is no term representing temperature)

(ii) It is proportional to the volume of atoms in the material (α_e - R³).

(iii) Electronic polarisation takes place in all dielectrics.