Energy Band Diagram

ENERGY BAND DIAGRAM

Fig. 3.3 shows a two-dimensional crystal structure of germanium and energy band representation of intrinsic semiconductor at very low temperature.

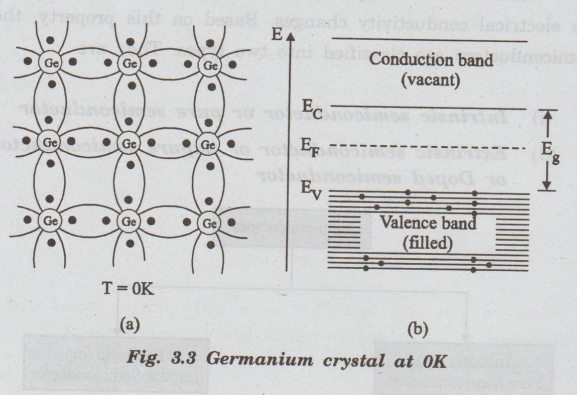
Fig. 3.3(a) Two-dimensional representation of germanium solid. divibuba No free electron is available as all the valence electrons are engaged in covalent bonds.

Fig. 3.3(b) Energy band representation. Valence band is fully ni nost occupied and conduction band is completely vacant.

At very low temperature say 0K, no free electrons are available for conduction. Hence, this semiconductor behaves as an insulator at very low temperature.

Charge carriers in intrinsic semiconductor

To get free electrons, covalent bonds must be broken. There are many ways of breaking covalent bond and setting the electrons free. One such way is to increase crystal temperature above 0K.

When the temperature of intrinsic semiconductor is increased, some of the electrons get sufficient energy to break covalent bonds.

Once the electrons are liberated from bond, they become free electrons. These free electrons move randomly through crystal. (Fig. 3.4(a))

As shown in fig. 3.4 (b), the energy required to break a covalent bond and to set an electron free is equal to band gap energy E_g. It is about 0.72 eV for germanium and 1.1 eV for (d) silicon.

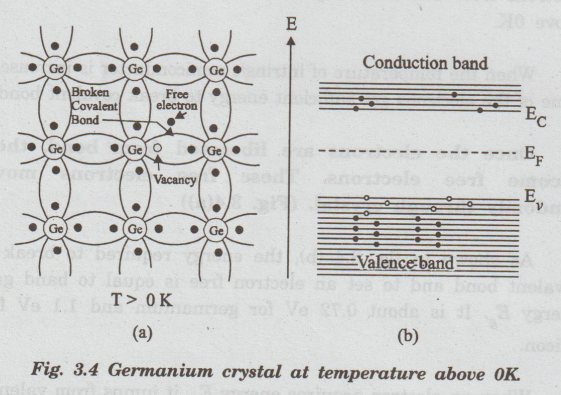
When an electron acquires energy E, it jumps from valence 'g' band to conduction band. As a result, a vacant site (empty space) is created in valence band.

This vacant site is called as a hole. The absence of an electron in covalent bond is known as hole. A hole can attract an electron and hence it acts as a positive charge.

When an electrical field is applied, these free electrons acquire directional motion and contribute to electrical conductivity.

For every electron freed from covalent bond, one hole is created in the crystal. It is relatively easy for a valence electron in a neighbouring atom to leave its covalent bond and fill this hole.

As a result, an electron moving from a covalent bond to fill a hole leaves behind a hole in its original position.

The hole effectively moves in a direction opposite to that of an electron. The hole in its new position may now be filled by an electron from another covalent bond.

Thus hole will correspondingly move one more step in the direction opposite to the motion of the electron.

(a) Thermal vibrations of atoms lead to breaking up of covalent bonds. Consequently, a free electron and a vacancy are produced simultaneously.

(b) Energy band representation. Energy E (=E-E) causes elod transition of electrons from valence band to conduction evithe band, leaving vacancies (hole) behind.

Therefore, in intrinsic semiconductor, current conduction is due to the movement of both electrons and holes.

Here, the number of electrons is equal to the number of holes at any given temperature.