Gauss's law and Boundary condition

GAUSS'S LAW AND BOUNDARY CONDITION

Gauss's law is an important basic law in electrostatics.

This law relates the electric flux through any closed surface and net charge available inside the closed surface.

Statement

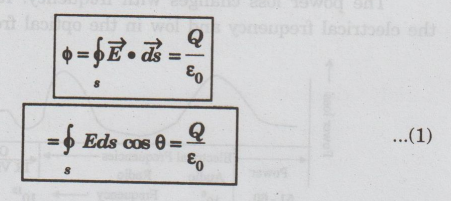
The total electric flux of the electric field  over any closed surface is equal to1/ ε₀ times the total charge enclosed by the surface.

Explanation

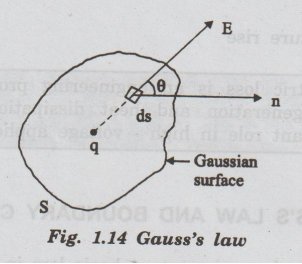
Let q be the net charge enclosed within a surface. This closed surface is known as "Gaussian surface" and it is an imaginary surface (Fig. 1.14).

The total electrical flux of  through a closed surface 'S' depends only on the value of the net charge inside the surface. The electric flux does depend not on the location of the charges inside the closed surface.

The charges outside the surface will not contribute to the flux. (ie., the flux through the closed surface due to the charges present outside the closed surface is zero).

Uses of Gauss's law

(i) It is used to find the electric field by constructing a closed surface (Gaussian surface).

(ii)Gauss's law is one of the fundamental equations of electromagnetic theory. i.e., it is one of the Maxwell's equations.

(iii) The Coulomb's law can be derived from Gauss's law.

Applications of Gauss's law

It is used to find electric field due to the given charge distributions.

Boundary Conditions

Consider the field in the parallel plate capacitor in figure 1.15 with out dielectric medium. A thin rectangular Gaussian surface is taken. This surface just encloses the positive electrode that contains the free charges +Q₀ on the plate.

The field E₀ is normal to the inner surface (area A) of the Gaussian surface. It is assumed that E₀ is uniform across the plate surface. Therefore the integral of E_n dA in equation (1) over the surface is simply E₀A. There is no field on the other faces of this rectangular Gaussian equation (1).

From Gauss Law

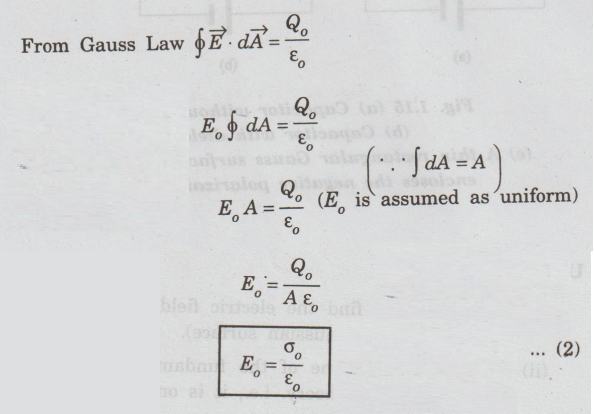
where, σ_v = Q₀ / A is the free surface charge density.

Now, let us consider that a dielectric slab partially fills the distance between the plates, as shown in figure 1.15(b).

The applied voltage remains the same, but the field is no longer uniform between the plates.

There is an air-dielectric boundary. The field is different in the air and dielectric regions.

Both these fields are normal to the boundary by the choice of the dielectric shape (faces parallel to the plates).

The bound surface charges + A σ_P , and -A σ_P, appear on the surfaces of the dielectric slab due to polarizatin as shown in figure 1.15. The surface charge density (σ_p) due to induced charge is equal to the polarization (P) in the dielectric. A very narrow rectangular Gaussian

From Gauss law

E₂ A- E₁A =- A σ_P / ε₀...(3)

where E₁ and E₂ are electric field in air and dielectric respectively - ve sign is due to negative induced change.

rearranging eqn (3)

E₁=E₂+ P / ε₀  ................(4)

(σ_p=P)

The polarization P and the field E₂ in the dielectric are related by

P= ε₀ X_e2E₂

or P = ε₀ (ε_r2 -1) E₂ ...(5)

where X_e2 is the electrical susceptibility and ε_r2 permittivity of the inserted dielectric. Substituting (5) in (4).

We have

E₁ = E₂+ (ε_r2 -1) E₂

E₁ = E₂+ε_r2 E₂-E₂

E₁ = ε_r2 E₂... (6)

(a) Boundary conditions between dielectrics

(b) The case for E_t1 = E_t2

E₁ = ε_r2, E₂...(7)

The field in the air part is E₁ and the relative permittivity is1.

The example in figure 1.15 involved is a boundary between air and a dielectric solid. The boundary is parallel to the plates and hence normal to the fields E₁ and E₂.

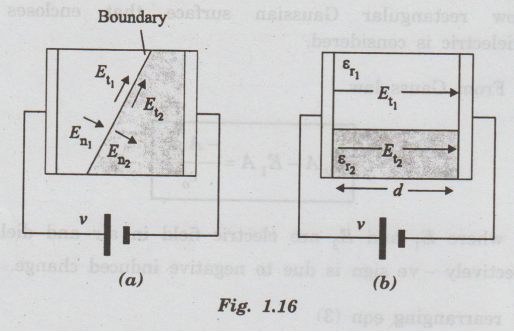
A general expression can be shown to relate the normal component of the electric field, shown as E_n1 and E _n2 in figure 1.16 on either side of a boundary by

ε_r1 E_n1 = ε_r2 E_n2 ...(8)

There is a second boundary condition that relates the tangential components of the electric field, shown as E_t1 and E_t2 in figure 1.16(b), on either side of a boundary. These tangential fields must be equal.

E_t1 = E_t2 ....(9)

The above boundary conditions are widely used in explaining dielectric behavior when boundaries are involved.

Classification of dielectric materials

Dielectric materials are classified based on the physical state as

(i) Solid dielectric materials

(ii) Liquid dielectric materials

(iii) Gaseous dielectric materials

Types of Dielectrics

Based on the applications, there are two types of dielectric materials

(i) Active dielectrics (Ferroelectrics, piezoelectrics and pyroelectrics)

 (ii) Passive dielectrics (electrical insulating materials)

Active dielectrics or Ferroelectric materials

Active dielectrics are the materials which are used to generate, amplify, modulate and convert the electrical signals. They are used to store electrical energy.

Passive dielectrics (Insulating materials)

The function of the insulating material is to obstruct the flow of electric current.