Hall effect

HALL EFFECT

The electrical conductivity measurements are not sufficient for the determination of number of charge carriers and their mobilities.

• Moreover, these measurements do not indicate whether current conduction is due to electrons or holes.

• Hence, it is very difficult to distinguish between p-type and n-type semiconductors. Besides, the electrical conductivity measurements do not give any information about the sign of the majority (p type or n type) charge au digcordi carriers.

• Therefore, Hall effect is used to distinguish between two types of charge carriers (electrons and hole). It also provides information about the sign of charge carriers.

Statement

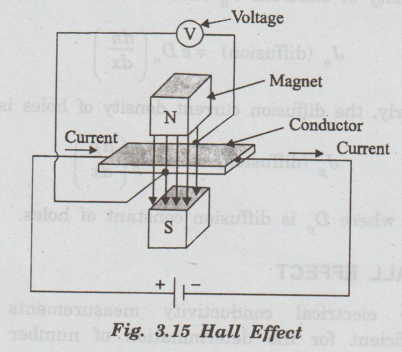
When a conductor carrying a current (I) is placed perpendicular to a magnetic field (B), a potential difference is produced inside the conductor in a direction perpendicular to both current and magnetic field. (Fig. 3.15)

This phenomenon is known as Hall effect. The voltage thus generated is called Hall voltage

Hall effect in n- type semiconductor

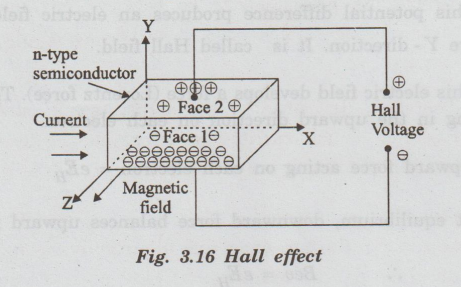
Consider a a n-type semiconductor in the form of a rectangular slab. In this slab, the current flows in X - direction and magnetic field B is applied in Z-direction. Due to Hall effect, voltage is developed along Y- direction as shown in fig. 3.16.

The current flow is entirely due to the flow of electrons moving from right to left along X-direction.

fetic field (B) is

When a magnetic field (B) is applied in Z-direction, then the electrons moving with velocity v experience a downward force.

Downward force experienced by the electrons = Bev …. (1)

This downward force deflects the electrons in downward direction. Hence, there is an accumulation of negative charge (electrons) on the bottom face of the slab (fig 3.17).

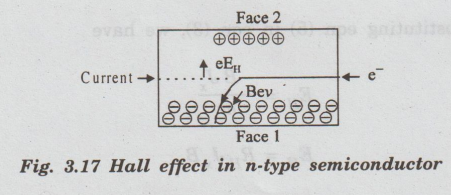
It causes bottom face to be more negative with respect to top face.

Now, a potential difference is developed between top and bottom faces of the slab.

This potential difference produces an electric field E in negative Y- direction. It is called Hall field.

This electric field develops a force (Lorentz force). This force is acting in the upward direction on each electron.

Upward force acting on each electron = еE_H ….(2)

At equilibrium, downward force balances upward force.

Bev = eE_H

E_H =  Bu ...(3)

The current density (J_x) along X-direction is related to velocity v as

J_x = - nev ...(4)

where n is concentration electrons.

v = -J_x / ne ...(5)

Substituting eqn (5) in eqn (3), we have

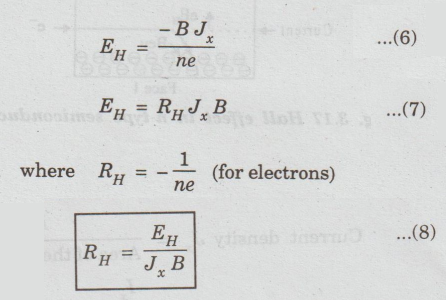
R_H is a constant and it is known as Hall coefficient.

The negative sign indicates that the electric field is developed in negative Y - direction.

Hall effect in p-type semiconductor

Similar to n-type semiconductor, we can write for p-type semiconductor

E_H = R_H J_x B

where Hall coefficient.

RH = + 1 / pe

where p is concentration of holes.

The positive sign indicates that the electrical field (Hallfield) is developed in positive Y - direction.

Hall coefficient in terms of Hall voltage

If t is the thickness of the sample and V_H is the voltage developed, then

V_H = E_H t

where E is Hall field. ...(1)

V_H = R_H J_x B t ...(2)

If b is breadth of the sample, then

Cross sectional area of the sample (A)

= Breadth (b) × Thickness (t)

= bt

Current density J_x  = I_x / Area of the sample (A)

= I_x / bt  …. (3)

Substituting eqn (3) in eqn (2), we get

V_H  = R_H I_x Bt / bt

V_H  = R_H I_x B / b

Hall coefficient RH = V_H b / I_x B ...(4)

Note:

For n-type, the polarity (sign) of V_H is opposite to that of p-type.

Determination of Hall coefficient

The experimental arrangement to measure Hall-coefficient is shown in fig. 3.18.

A semiconductor is taken in the form of a rectangular slab of thickness t and breadth b. A suitable current I, ampere is passed into this sample along X-axis by connecting it to a battery.

Now, it is placed in between north and south poles of an electromagnet. The magnetic field is applied along Z-axis.

Due to Hall effect, Hall voltage (V) is developed in the sample. This voltage is measured by fixing two probes at the centers of the bottom and top faces of the sample.

By measuring Hall voltage, Hall coefficient is determined from the formula

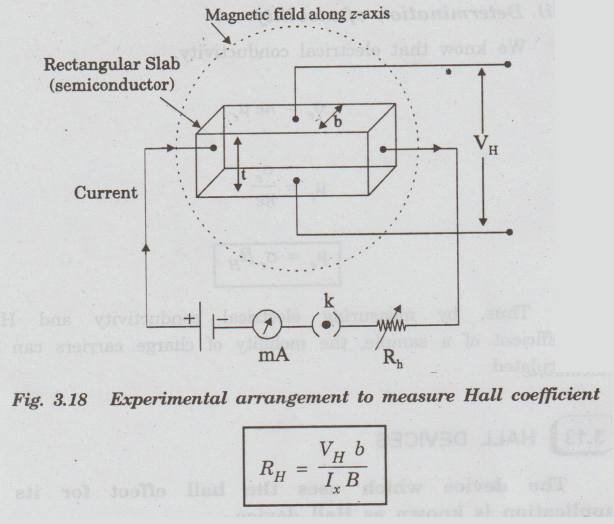
From Hall coefficient, carrier concentration and mobility can be determined.

Applications of Hall effect

 (i) Determination of semiconductor type

The sign of the Hall, coefficient is used to find whether a given semiconductor is n-type or p-type.

(ii) Calculation of carrier concentration

By measuring Hall coefficient R_H, carrier concentration is determined from the relation

n = 1 / eR_H

(iii) Determination of mobility

We know that electrical conductivity,

σ_e = ne μ_e

µ_e  = σ_e / ne

µ_e  = σ_e R_H

Thus, by measuring electrical conductivity and Hall coefficient of a sample, the mobility of charge carriers can be calculated.