Local field or Internal field

LOCAL FIELD OR INTERNAL FIELD

When a dielectric material is placed in an externa electrical field, it produces an induced dipole moment.

Now, there are electrical fields acting at any point inside dielectrics.

(i) macroscopic electric field due to external electrical field

(ii) electrical field due to electric dipole moment

This long-range coulomb electrical field produced due to dipoles is known as internal field or local field.

It is responsible for polarisation of each atom or molecule in a solid.

Lorentz method to find internal field (Derivation)

The dielectric material is uniformly polarised by placing it in between two plates of a parallel plate capacitor (uniform electrical field) as shown in fig. 1.10.

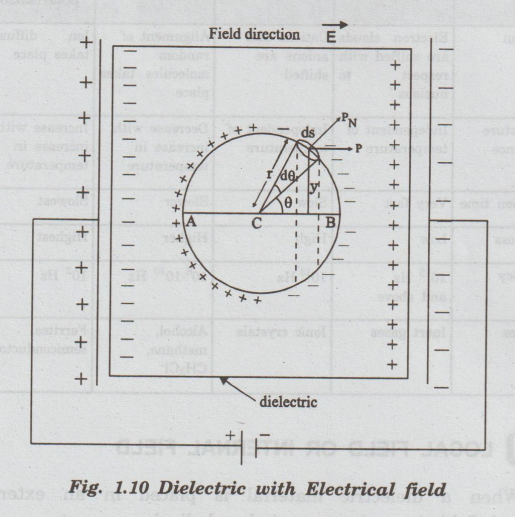
To find internal field acting on an atom at C of dielectric, let us consider an imaginary small spherical cavity around the atom.

The internal field (E_int) at the atom site is considered to be resultant of the following four components. E₁, E₂, E₃ and E₄

i.e., E_int = E₁+E₂+E₃+E₄... (1)

where

E₁ → Electrical field due to charges on the plates of the capacitor (without dielectric)

E₂ → Electrical field due to polarised charges (induced charges) on the plane surface of the dielectric

E₃ → Electrical field due to polarised charges induced on the surface of the imaginary spherical cavity (to be calculated)

E₄ → Electrical field due to permanent dipoles of atoms inside the spherical cavity considered

Macroscopically, we can take E = E₁ +E₂ i.e., the electrical field externally applied (E₁) and the electrical field induced on the plane surface of the dielectric (E₂) is considered as a single electrical field (E).

If we consider a dielectric that is highly symmetric, the electrical field due to dipoles present inside the imaginary cavity will cancel out each other. Therefore, the electrical field due to permanent dipoles present inside the cavity E₄ = 0.

Now, the equation (1) reduces to

E_int = E+E₃ .....(2)

Calculation of E3

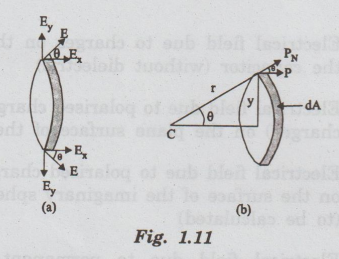
Let us consider a small area ds on the surface of spherical cavity. It is confined within an angle dθ at an angle θ in the direction of electrical field E.

Polarisation (P) is parallel to E. P_N is the component of polarisation perpendicular to the area ds as shown in fig. 1.11.

P_N = P cos θ

q' is the charge on the area ds.

Polarisation is also defined as the surface charges per unit area

P_N = q'/ ds

P_N = P cos θ = q' / ds

Charge on ds, q'= P cos θ ds.............(3)

Electrical field intensity at C due to charge q' (Coulomb's law) is given by

E = q' / 4 πε_or²

Substituting for q' from the eqn (3), we have

E = P cos θ ds / 4πε_or²......(4)

This electrical field intensity is along the radius r and it is resolved into two components (E_x and E_y) as shown in fig. 1.11(a).

The component of intensity parallel to the electrical field direction

E_x = E cos θ ....(5)

Substituting E from eqn (4) in eqn (5), we have

E_x = P cos θ ds cos θ / 4 πε_or²

E_x= P cos² θ ds/4 πε_or².....(6)

The component of intensity perpendicular to the field direction,

E_y = E sin θ

Since the perpendicular components are in opposite directions [fig. 1.11 (a)], they cancel out each other. Hence, the parallel components alone are taken into consideration.

Now, consider a ring of area dA which is obtained by revolving ds about AB [fig. 1.11 (b)].

Electrical field intensity due to charges present in the whole sphere is obtained by integrating equation (9) within the limits 0 to л. This electric field is taken as E₃.

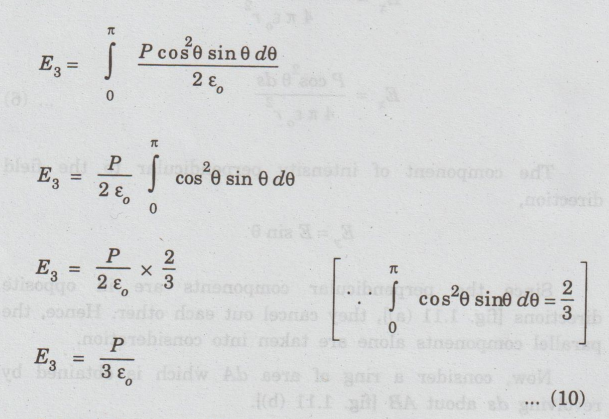
Substituting eqn (10) in eqn (2), we get

E_int = E+ P / 3ε₀ ......(11)

E_int is the internal field or Lorentz field.

The equation (11) shows that E_int is larger than the macroscopic field intensity E. Hence, the molecules are more effectively polarised.