Electric Circuit Analysis: Unit II: Network Reduction and Theorems for dc and ac Circuits
Network Reduction and Theorems for dc and ac Circuits
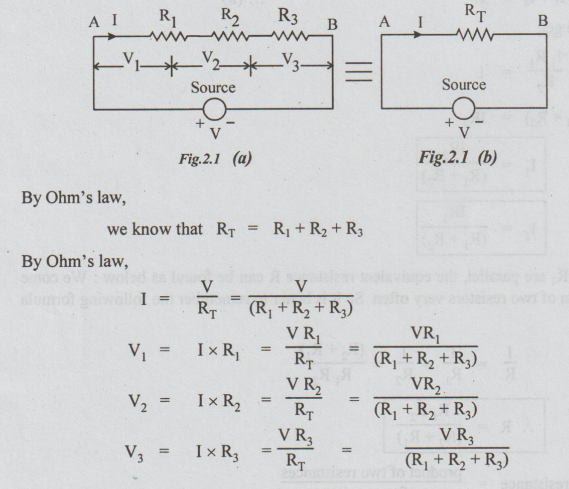
To find the expressions for the voltages V1, V2 and V3 in terms of V, R1, R2, R3
Unit - II
NETWORK REDUCTION AND THEOREMS FOR DC AND AC CIRCUITS
VOLTAGE DIVISION:
To
find the expressions for the voltages V1, V2 and V3 in
terms of V, R1, R2, R3 for
Current
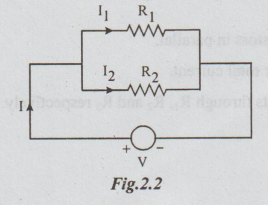
division formula:
(a)
In many cases, we will have only two resistors connected in parallel
Let
these resistors be R1 and R2 as shown in the Fig.2.2.
The
total current = I
Current
through R1 = I
Current
through R2 = I2
To
express I1,
and I2,
in terms of I, R1 and
R2.
Note:
In case R, and R2 are parallel, the equivalent resistance R can be found as
below: We come across parallel combination of two resistors very often. So it
is better to remember the following formula for R.
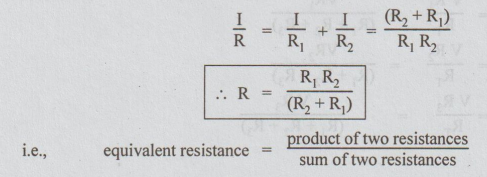
The
reader is to note that the above formula is true only for two resistances in
parallel.
(b)
When three resistors are in parallel: To find
equivalent resistance and the expressions for branch currents. Refer Fig.1.12
Let
R1, R2 and R3 be the resistors in parallel.
Let
I be the supply current or total current.
Let
I1, I2 and I3 be the currents through R1,
R2 and R3 respectively.
To
find the currents I1,
12 and 13
:
Given R1, R2, R3 and I.
We
know that,
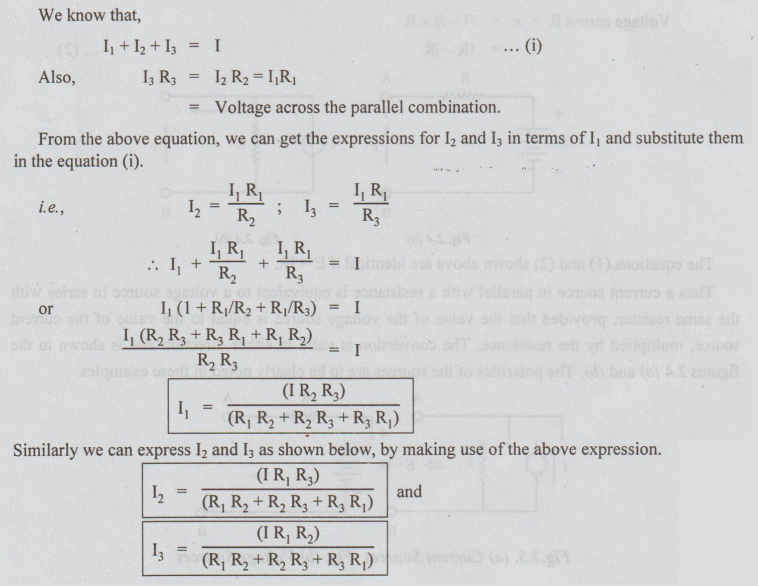
Note:
1.
If there are n resistors each of R ohms connected in parallel, the equivalent
resistance is RT = R / n
2.
For getting more resistance we need series combination.
3.
For getting lesser resistance we need parallel combination.
Electric Circuit Analysis: Unit II: Network Reduction and Theorems for dc and ac Circuits : Tag: : - Network Reduction and Theorems for dc and ac Circuits
Electric Circuit Analysis: Unit II: Network Reduction and Theorems for dc and ac Circuits
Under Subject
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Related Subjects
Professional English II
HS3251 2nd Semester 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Statistics and Numerical Methods
MA3251 2nd Semester 2021 Regulation M2 Engineering Mathematics 2 | 2nd Semester Common to all Dept 2021 Regulation
Engineering Graphics
GE3251 eg 2nd semester | 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Physics for Electrical Engineering
PH3202 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Basic Civil and Mechanical Engineering
BE3255 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Physics for Electronics Engineering
PH3254 - Physics II - 2nd Semester - ECE Department - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Electrical and Instrumentation Engineering
BE3254 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Circuit Analysis
EC3251 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Materials Science
PH3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Physics for Civil Engineering
PH3201 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Basic Electrical, Electronics and Instrumentation Engineering
BE3252 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Physics for Information Science
PH3256 2nd Semester CSE Dept | 2021 Regulation | 2nd Semester CSE Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation
Programming in C
CS3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation