Norton's Theorem

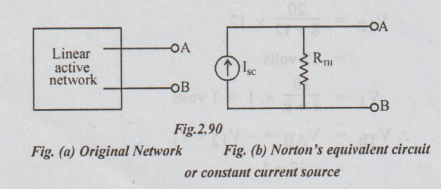
Norton's Theorem

Norton's theorem is the dual of the Thevenin's Theorem :

Statement: "Any linear active network with output terminals A, B as shown in the figure can be replaced by a single current source. ISC (IN) in parallel with a single impedance ZTh (Zn) = RTh (RN)"

ISC is the current through the terminals AB of the active network when shorted. ZTh is the Thevenin's impedance.

The current through an impedance connected to the terminals of the Norton's equivalent circuit must have the same direction as the current through the same impedance connected to the original active network.

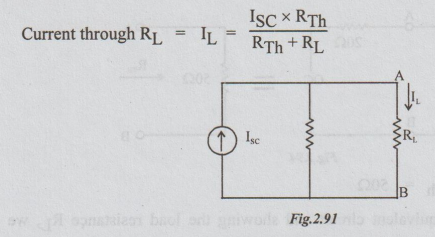
After evaluating the values of ISC and RTh, the current through RL connected across A and B can be calculated by applying division of current formula which is expressed below:

WORKED EXAMPLES

Example 1 Determine the voltage across 2002 resistor in circuit by Norton's theorem.

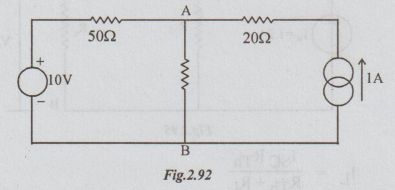
Solution: Step 1: To find the short circuit current ISC. Replace the 200 2 by short circuit. The current through short circuited AB is ISC. Refer the following figure.

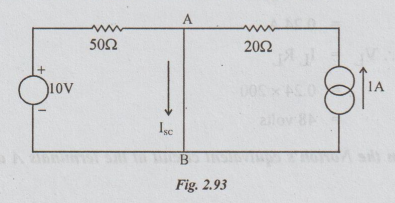
The voltage source will drive a current of 10/50 = 0.2 A, which flows through short circuited AB only. Similarly the current of 1A flows through 20 and then through short-circuited AB only. 0.2 A will not flow through 20 Ω and 1A will not flow through 50 Ω. It is because of short-circuit. So, ISC = 0.2+1= 1.2A.

Step 2: To find RTh: From the given circuit, disconnect RL = 200 Ω between A and B and also kill the sources. The resultant circuit becomes as below:

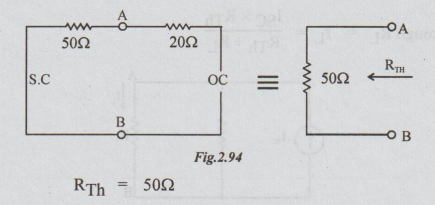
Step 3: Drawing Norton's equivalent circuit and showing the load resistance RL, we get the following circuit:

Example 2 Obtain the Norton's equivalent circuit at the terminals A and B for the network shown.

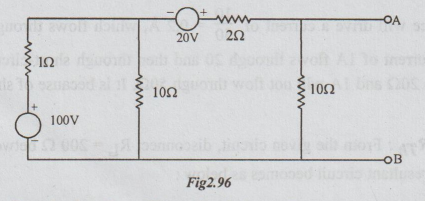
Solution: Step 1: To calculate ISC: Short circuit A and B terminals to get the following circuit.

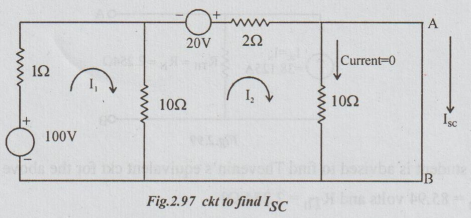
As 10 Ω is shorted, no current flows through it. Hence ISC = I2. Neglect presence of 10 Ω. By inspection,

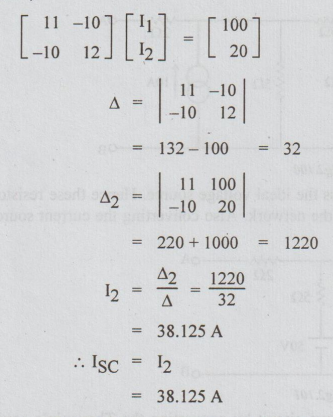
Step 2: To find RTh: From the original circuit kill the sources. Remember that 100 must be taken and it is effective.

Step 3: Norton's equivalent circuit is

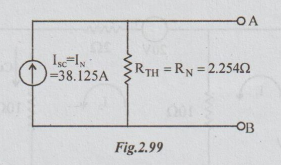
 [Note: The student is advised to find Thevenin's equivalent ckt for the above problem.]

 [Ans: VTh = 85.94 volts and RTh = 2.254 Ω]

Example 3 Obtain the Norton's equivalent circuit at the terminals A and B for the network shown.

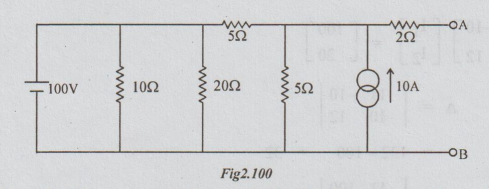
Solution: 10 Ω and 20 Ω are connected across the ideal voltage source. Hence these resistors can be removed without altering the performance of the network. Also converting the current source into voltage source we get the following circuit :

Norton's equivalent can be found for the above circuit by converting the Thevenin's equivalent source into current source. Or, we can directly find the Norton's equivalent which is done as below:

Step 1: To find short-circuit current. Short circuit the terminals A and B to obtain the following circuit:

By loop current method, we can write that

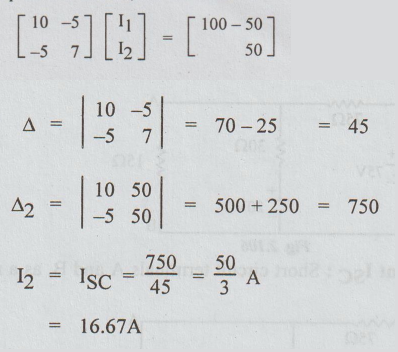
Step 2 : To find RTh : Killing the sources and keeping A and B terminals open, we get

[Note : The student is advised to solve the above problem without removing the resistance of 10 Ω and 20 Ω. He can convert the current source into voltage source, for convenience.]

Example 4 Find the voltage across the 15 Ω resistor using Norton’s theorem for the circuit given below:

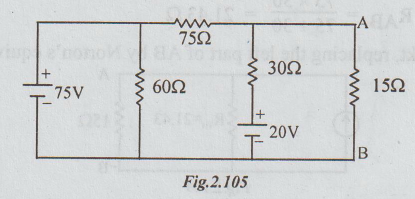
Solution : Here also since 75V is the ideal voltage source, 60 Ω resistor can be removed without altering the performance of the circuit. The resultant figure is re-drawn as below:

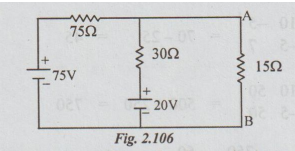
Step 1: To find Norton's current ISC : Short circuit terminals A and B, as a result of which the circuit becomes as below:

Step 2: To find RTh:

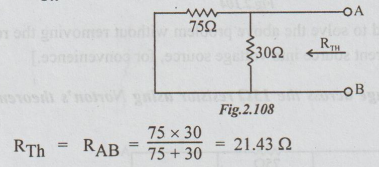
Step 3: In the original ckt, replacing the left part of AB by Norton's equivalent we get,

Example 5 Obtain Norton's equivalent across terminals A and B for the network shown below:

Solution: Step 1: To calculate ISC : Short-circuit terminals A and B to obtain the following circuit.

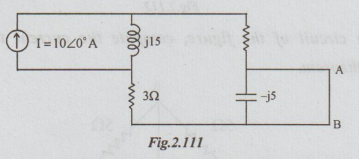
Since the capacitor is short circuited there is no current flow through it. The source current is divided into two parallel paths. A part of I flows through series combination of 20 and 30 which is also ISC. Remaining of I flows through j15 Ω.

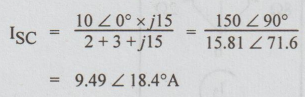
Step 2: To find ZTh: From the original circuit kill the energy source. i.e., Open circuit current source.

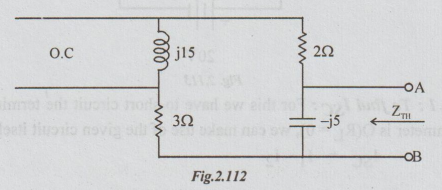
Between the terminals A and B there are two branches in parallel. The impedance of one branch is Z1= 5 + j 15.

The impedance of the other =

Step 3 : Norton’s equivalent circuit is

Example 6 In the circuit of the figure, compute the current through the O resistance ammeter. Use Norton’s theorem.

Solution :

Step 1 : To find ISC : For this we have to short circuit the terminals A and B. As the resistance of the ammeter is O(RL = 0), we can make use of the given circuit itself to find ISC.

ISC = I1 ~ I2

By inspection,

Step 3: Norton's equivalent circuit

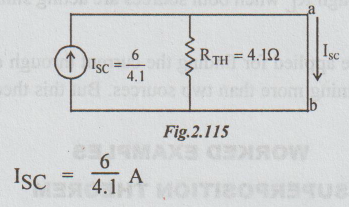
ISC = 6/4.1 A

[Note: The current through the zero resistance ammeter is ISC which was found by loop current method. There is no need of RTh. But to let the student to know as how to apply Norton's theorem through a short circuited path, the problem is solved by this method.]