Reciprocity Theorem

5. Reciprocity Theorem

Statement: In a linear, bilateral network a voltage source V volts in a branch gives rise to a current I, in another branch. If V is applied in the second branch, the current in the first branch will be

I. This V / I is called transfer impedance or resistance.

On changing the voltage source from branch 1 to branch 2, the current I in the branch 2 appears in branch 1.

WORKED EXAMPLES

Example 1 For the circuit shown in the figure below, find 13 and verify reciprocity theorem.

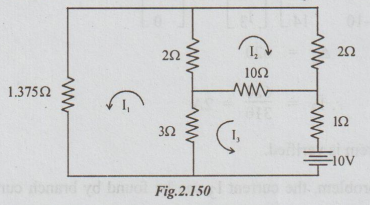
Solution: Step 1: By inspection putting in the matrix form, we get

Step 2: Transferring the battery, to the branch with 1.375 Ω resistor, the following circuit is obtained. The current through 1 Ω is taken as I3. According to reciprocity theorem this I3 = 2A.

Let us calculate the value of I3 in figure below:

Thus reciprocity theorem is verified.

Note: In the above problem, the current 13 can be found by branch current method. In that case both KCL and KVL are to be applied. It is solved here by loop current method, where only KCL is to be applied. This method is preferred to loop current method.

Example 2 Verify reciprocity theorem in the circuit shown in the figure and also calculate the transfer resistance.

Solution: Step 1:

Voltage across 8 ohms = V = Ig × R

But Ig = 10 × 2 / 2 + 8 = 2A

R = 8Ω

V = 2 × 8 = 16V

Step 2: Interchanging the current source and response, the circuit becomes as below: Here the response is V.

V = I2 × R, R = 2Ω, since the current 2

In both cases, the ratio of voltage to current is the same. Hence the reciprocity theorem is verified.

The transfer resistance = V/ I = 16/10 = 1.6Ω

Example 3 In the network shown in the figure, the voltage source 100 ∠ 45°V causes current Ix in the 5Ω branch. Find Ix and then verify the reciprocity theorem for this circuit.

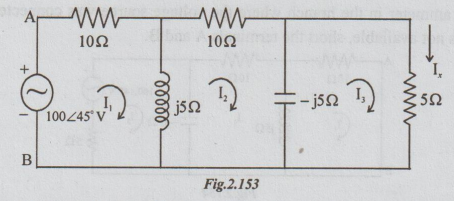
Solution: Step 1: It is required to find the value of Ix. Let us apply loop current method. If the loop currents are taken to be I1, I2 and I3 as shown, then Ix = I3.

For the above circuit, by inspection, we can write that

Step 2: Now connect the voltage source in the branch in which the current is I, i.e., in 52 branch and connect an a.c. ammeter in the branch where the voltage source was connected earlier as shown below. If ammeter is not available, short the terminals A and B.

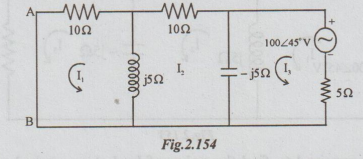
If the current through AB is same as the value of Iy in the step 1, we can say that the reciprocity theorem is verified. To calculate the current let us again prefer loop current method to other methods.

By inspection.

Hence the reciprocity theorem is verified.

Example 4 In the circuit shown determine Vx Then apply the reciprocity theorem and compare the 2 voltages.

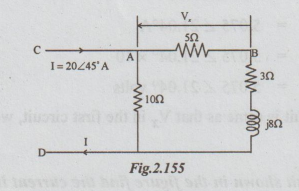
Solution : Step 1 : Vx = I5 × 5

Is is the current through the series combination of 5Ω, 3Ω and j8Ω.

I5 = 20 ∠ 45° × 10 / 10 + 5 + 3 + j8

= 200 ∠ 45° / 19.7 ∠ 23.96°

= 10.15 ∠ 21.04°A

Vx = 10.15 ∠ 21.04° (5 ∠ 0°)

= 50.75 ∠ 21.04° V

Step 2: Connecting the current source across 5 and voltmeter across C and D, the circuit becomes as:

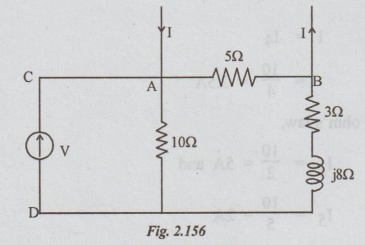
The voltage across CD = V = Voltage across 10Ω

To find the voltage across 10Ω, current through it must be known. As is shown in the circuit, the source current I is divided into two parallel paths. A part of I flows through 5Ωand remaining flows through the series combination of 10Ω, j8Ω and 3Ω.

By current division formula current through 10Ω = I10

= 20 ∠ 45° × 5 / 10 + j 8 + 3 + 5

= 100 ∠ 45° / 18 + j8

= 100 ∠ 45° / 19.7 ∠ 23.96

= 5.075 ∠ 21.04°A

V = 5.075 ∠ 21.04° × 10

= 5.075 ∠ 21.04° volts

As this V in the second circuit is same as that Vx in the first circuit, we can say that the reciprocity x theorem is verified.

Example 5 In the circuit shown in the figure find the current in the 42 resistor. Apply the reciprocity theorem and compare the 2 currents. What change results in the current through 5Ω and 2Ω branches?

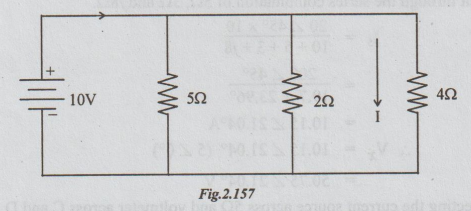
Step 1: In the given circuit, the resistors 402, 22 and 502 are all in parallel across the 10V source. As shown

I = I4

= 10 / 4 = 2.5 A

Similarly by applying ohm's law,

I2 = 10 / 2 = 5 A and

I5  = 10 / 5 = 2A

Step 2: Connecting the voltage source in the 452 branch and D.C. ammeter (of negligible resistance) in place of the voltage source of the given circuit we get the following:

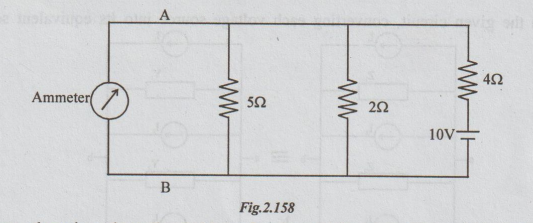
In this figure, there is a short circuit (through ammeter) between the parallel combination of 5Ω and 2Ω. Hence, no current will flow-through 5Ω and 2Ω. The current from the voltage source flows through only 4Ω and the same thing is read by the ammeter. By applying ohm's law, reading of ammeter 10/4 = 2.5A.

Thus, reciprocity theorem is verified for the given circuit.

[Note: After connecting the voltage source in 4Ω resistor, the current through branches of resistances 2Ω and 5 Ω becomes 0.]