Super Position Theorem

3. Super Position Theorem

With the help of this theorem, we can find the current through or the voltage across a given element in a linear circuit consisting of two or more sources. The statement is as follows:

"In a linear circuit containing more than one source, the current that flows at any point or the voltage that exists between any two points is the algebraic sum of the currents or the voltages that would have been produced by each source taken separately with all other sources removed."

Note:

1. Removal of an ideal voltage source means short circuiting.

2. Removal of an ideal current source means replacing it by an open circuit.

3. Removal of practical voltage source means replacing it by an internal resistance.

Example: Consider the following simple circuit.

Let E₁ be greater than E₂. I_L is the load current i.e., current through the load resistance. The net voltage in the circuit is equal to E₁-E₂.

Total resistance = r₁ + r₂ + R_L

Therefore, I_L= E₁-E₂ /  r₁ + r₂ + R_L

= (E₁ / r₁ + r₂ + R_L) + ( - E₂ / r₁ + r₂ + R_L)

I_L= I_L+ (-I_L’)

I_L' is the current flowing through R_L because of E₁ alone, flowing from A to B.

I_L" is the current flowing through R_L because of E₂ alone, flowing from B to A.

I_L is the current flowing through R_L when both sources are acting simultaneously.

Note:

Superposition theorem can be applied for finding the current through or voltage across a particular element in a linear circuit containing more than two sources. But this theorem can not be used for the calculation of the power.

WORKED EXAMPLES

SUPERPOSITION THEOREM

Example 1 Compute the current through 23 ohm resistor of the figure below by using superposition theorem.

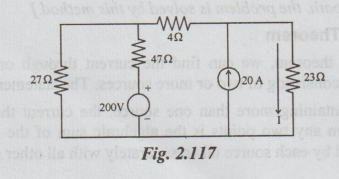
Solution: Step 1: Allow only the voltage source to act. The corresponding circuit is as below:

The resistance connected to the source = 47 + 27 × 27 / 27+ 27

= 60.5 ohms

Total current from the source = 200 / 60.5 = 3.306 A

The current through 23 ohms = IL = 3.306 × 27

= 1.653 A

Step 2: Allow only the current source to act. The circuit becomes as

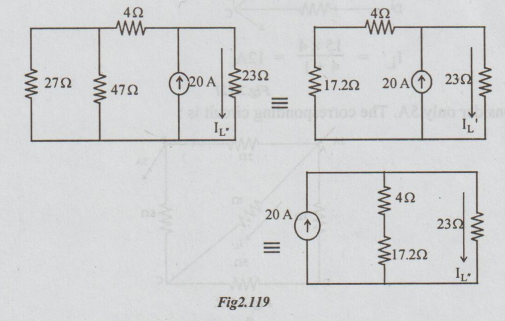
IL = 20 × 21.2 / 21.2 + 23 = 9.6 A

By superposition theorem, IL = IL + IL “ = 1.653 + 9.6 = 11.253 A

[Note: The directions of IL' and IL

Example 2 Using superposition theorem, find the current in resistance R3 in the circuit shown below.

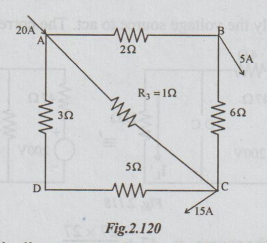
Solution: The above circuit diagram may be assumed to be consisting of two currents. One current of 15 A entering at A and leaving at C. Another current of 5A, entering at A and leaving at B.

Step 1: Consider only 15A. The relevant circuit diagram is as below:

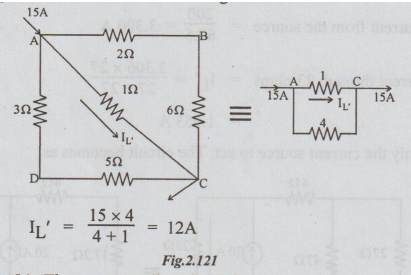
Step 2: Consider only 5A. The corresponding circuit is:

1Ω and 8Ω are in parallel. Their equivalent is 8/9 = 0.9Ω 0.9Ω and 6Ω are in series, equal to 6.9Ω.

Example 3 Find the current in the 22 resistor between A and B for the network using superposition theorem.

Solution: Step 1: When only 10V source is acting:

Let the current through 202 be IL'. The circuit diagram with 10V source acting, and 20V source killed is as below:

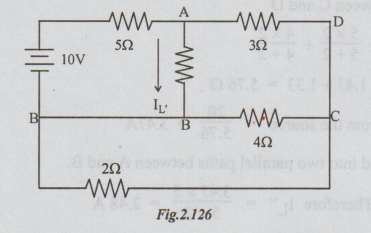
Between B and C, 2Ω and 4Ω are in parallel. Their equivalent = 2 × 4 / 2 × 4 = 1.33 Ω. Now, the circuit diagram can be re-drawn as below:

For the above circuit, the total resistance connected to the 10V source = 5 + 2 × 4.33 / 2 + 4.33 = 6.37 Ω.

Current from the source = 10 / 6.37 = 1.5 A

Therefore IL' = 1.57 × 4.33 / 2 + 4.33

= 1.07 A

Step 2: Allow only 20V source to act, killing the other source. The circuit becomes as :

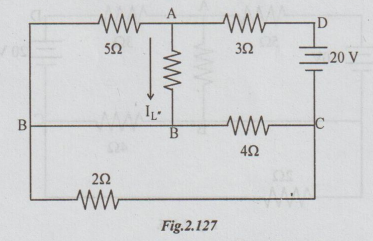
By inspecting the above figure, we can say that across the voltage source 20V, there is series parallel combination of resistances.

Between A and B, 2022 and 502 are in parallel. Between B and C 42 and 202 are in parallel. So, the equivalent resistance between C and D

= 3 + (5 × 2/ 5 + 2) +( 4 × 2 / 4 + 2)

= 3 + 1.43 + 1.33 = 5.76 Ω

The current from the source = 20 / 5.76 = 3.47A

This current is divided into two parallel paths between A and B.

Therefore IL" = 3.47 × 5 / 5 + 2 = 2.48 A

By applying superposition theorem, the current through 2 Ω connected between A and B = IL = IL' +IL' = 1.07 + 2.48 = 3.55A.

Example 4 Find the current in the branches A, B, C of the following 2 source network. Apply superposition principle.

Solution: Step 1: When only V source is acting, I source becomes open circuit. Refer fig .2.128 (b). The current from V source flows only through 2Ω and 2Ω. No current flows through 4Ω as open circuit

I1 = 4 / 2 + 2 = 1A.

Step 2: Allow only the I source to act, then V source becomes short circuited. For circuit refer fig.2.66 (c). The source current of 2A flows through 42 and is divided into two paths. The currents shown in the figure are

Iɑ =  2 × 2 / 2 + 2

Ic = 2 - 1 = 1A

By applying superposition principle,

Current through branch A = I1 - 1ɑ = 1 -1 = 0

Current through branch C = I1 + Ic = 1 + 1 = 2A

Current through branch B = 2A

Example 5 Using superposition theorem or otherwise, obtain the current in EA in figure below:

Step 1: First allow only IV source to act. Let the current in EA be I'. The relevant circuit diagram is as below:

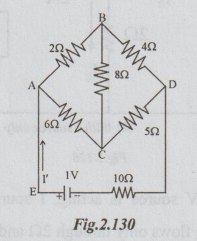
I' can be found by applying mesh current method or converting delta to star and then applying Ohm's law. The above circuit becomes as drawn below after converting delta connection between A, B and C into its equivalent star.

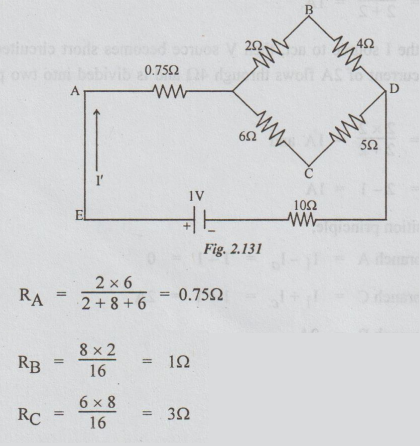
Total resistance connected across the source

= 0.75 + 5 × 8 / 5 + 8 + 10 = 13.83 Ω

I’ = voltage / resistance = 1/13.83

= 0.0723 A = 72.3 mA

It flows from E to A.

Step 2: When only 2V source is acting and the other source short circuited, the circuit becomes as shown in fig. 2.131. Now let the current in EA be I".

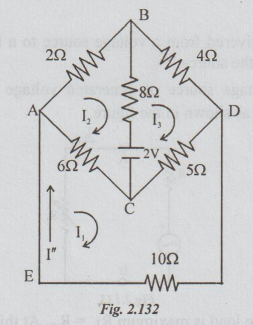
For the calculation of I", loop current method is applied. Let the loop currents be 11, 12 and 13 as shown in the figure above. I" = I1.

Step 3: By applying superposition theorem, the current through

EA = I = I' + 1'= 72.3 - 9.736 = 62.564 mA.