Thevenin's Theorem

NETWORK THEOREMS

1. Thevenin's Theorem

Consider the following active circuit.

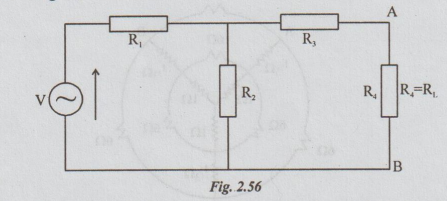
Suppose that the current through the load resistance R is required. It can be calculated by the following methods.

(a) Series parallel simplification

(b) Branch current method

(c) Loop current method

If the circuit consists of one more loop, in addition to the existing two loops, the first method will become more tedious. If R_L takes various values, whatever method you are applying it will be some what much laborious. For example, if you apply loop current method, we must form the matrix and solve for I_L. This procedure is to be repeated as many times as the values of R_L. The Thevenin's theorem helps us to avoid the repeated procedure. By this theorem we can replace a given active circuit between two terminals by a constant voltage source.

Then, by applying ohm's law, we can compute the value of I_L.

Statement of Thevenin's Theorem :

Any linear active network with output terminals A and B as shown in fig. 2.57 (a) can be replaced by a single voltage source (V_Th= Voc) in series with a single impedance (Z_Th = Zi)

V_Th is the Thevenin's voltage. It is the voltage between the terminals A and B on open circuit condition. Hence it is called open circuit voltage denoted by Voc

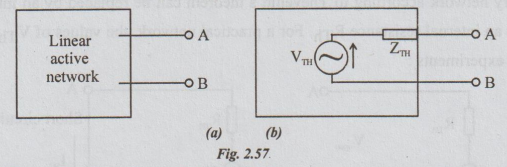
Z_Th is called Thevenin's impedance. It is the driving point impedance at the terminals A and B when all internal sources are killed. In case of D.C, Z_Th is replaced by R_Th

If a load impedance Z_L is connected across AB, we can find the current through it by the formula

I_L = V_Th / Z_Th+Z_L

Note: 1. This theorem can be applied for both D.C and A.C circuits.

2. In the Thevenin's equivalent circuit (Voltage source), if AB terminals are short circuited, the current flowing through AB is obtained by ohm's law. Refer fig. 2.93 (b).

Isc = V_Th / Z_Th ⇒ Z_Th = V_Th / I_SC

Steps to be followed in applying Thevenin's Theorem

The following steps are necessary in applying Thevenin's theorem for the given network:

1. Let the load resistance be R_L through which the current I_L is required. Mark the terminals A and B (for convenience) across which RL is connected. i.e., R_L is supposed to be connected between the terminals marked as A and B.

2. Blindly, draw the Thevenin's equivalent circuit between A and B terminals. It is a constant voltage source with voltage V_Th and resistance R_Th

3. In the given circuit disconnect R_L and redraw the fig. after removing R_L. Find the voltage or br between A and B. It is V_Th

4. From the circuit in the above step, kill all the energy sources properly and obtain the equivalent resistance between A and B when looked back. It is R_Th

R_Th can also be calculated in the following way:

(a) In a given circuit, replace R_L by short-circuit. Find the current through this. It is I_SC.

So, R_Th = V_Th / I_SC

Open and Short Circuit Method for finding Internal Z (Z_i = Z_Th) of a network

Every network according to Thevenin's theorem can be replaced by an internal source V_Th in series with an internal resistance R_Th. For a practical network, the values of V_Th and R_Th may be found by two experiments:

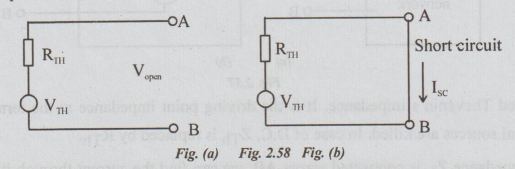
1. Keep the terminals open as shown in fig.2.58 (a). The voltage between the open terminals A and B is V_Th. It can be measured with a high resistance voltmeter, connected across the terminals.

2. Short circuit the terminals and connect an ammeter in series with the short-circuit. Refer fig. (b). The ammeter measures the short-circuit current I_SC. As the resistance of the meter is negligible, the ammeter does not affect the conditions of a short-circuit.

From fig. (b), ISC = V_Th / R_Th (by ohm's law)

Therefore, R_Th = V_Th / I_SC = open circuit voltage / short circuit current

These two tests are the ones which are generally employed to determine the network equivalent of electric machines such as transformer, alternator, induction motor and so on.

Power Calculation using Thevenin's Theorem

We have seen that this theorem replaces an active network by a voltage V_Th and a series resistance RTh, as far as any external load connected to the terminals of the network is concerned. For instance, if the load current is IL, then the power dissipated in R_L will be I²_L RL. As I_L is actual current, the power calculated will also be correct. That means, the theorem can be used to find the power in external circuit.

In the Thevenin's equivalent there is no current flow when the terminals are open. So, the internal power is 0. But in the actual network, even when the terminals are open, currents may flow because of some closed loops. Hence, there is power loss. We may call it no load power loss. The power calculations are true externally but not internally.

The power loss in the actual network and in its Thevenin's equivalent are not equal. But, the difference between the two losses is constant. It does not vary with change in the external load. The constant difference is the no-load power loss.

BOOT WORKED EXAMPLES

THEVENIN'S THEOREM

Example 1 Determine the current I in the network by using Thevenin's theore

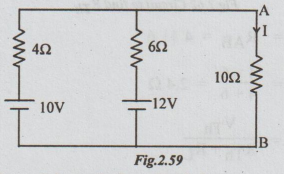
Solution: Step 1. The Thevenin's equivalent circuit is

Step 2: To find VTh: From the given circuit disconnect RL = 10 Ω

Step 3: To calculate RTh: From the above circuit, kill the sources. The resultant circuit is

Example 2 Find the Thevenin's equivalent for the network of the figure between a and b.

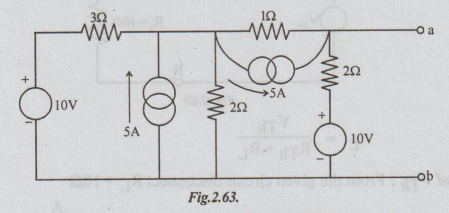
Solution: The network given is a combination of voltage and current sources. By converting voltage source into current source and vice-versa, wherever necessary and simplifying we can obtain the required network.

Step 1: Converting or transforming the voltage source of 10V in series with resistance 32 into equivalent current source, the following circuit is obtained.

Step 2: Replacing the 2 current sources in parallel by its equivalent current source, we get the following circuit.

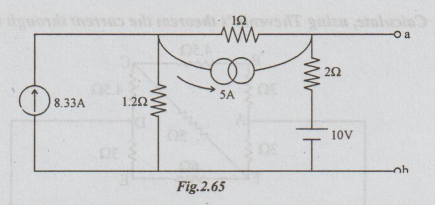
Step 3: Transforming the 2 current sources in series by their equivalent voltage sources we get the following network.

Step 4: Transforming the voltage sources which are parallel in the above circuit, into their equivalent current sources we get the following network.

Step 5: Converting the current source into equivalent voltage source, we get the Thevenin's equivalent circuit as shown below:

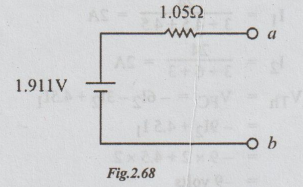
Note: From step 3, we can proceed to find VTh and RTh without going through step 4.

Example 3 Calculate, using Thevenin's theorem the current through the branch FC.

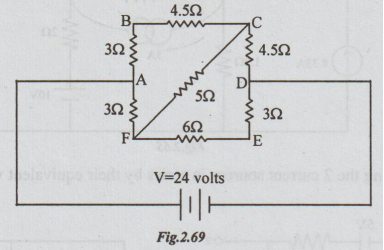
Solution: Step 1: The Thevenin's equivalent circuit is,

Step 2: To calculate VTh:

Disconnect RL = 5 Ω, between F and C terminals.

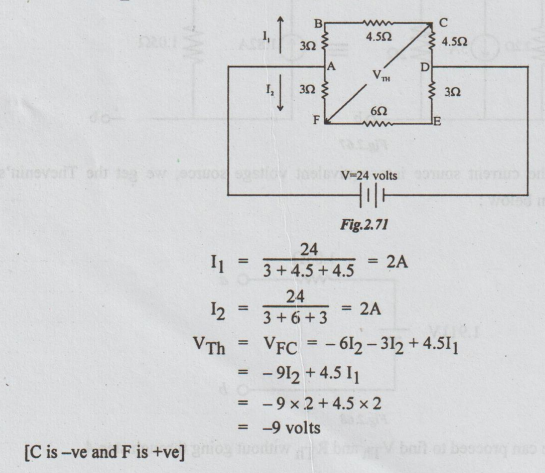
Step 3: To calculate RTh: Re-draw the above circuit, after killing the voltage source.

Example 4 It is required to find current through the 0.12 resistor in the figure, using Thevenin's method.

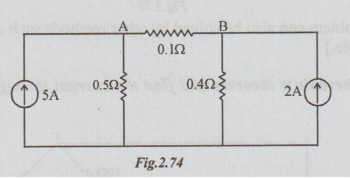
Solution: Step 1: The Thevenin's equivalent circuit :

Solution: Step 2: To calculate VTh: From the given network disconnect (remove) RL = 0.1 Ω

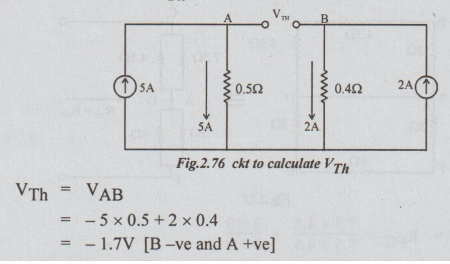
VTh = VAB

= -5 × 0.5 + 2 × 0.4

= -1.7V [B-ve and A +ve]

Step 2: To calculate RTh: Kill the current source in the above circuit by open circuit (O.C.)

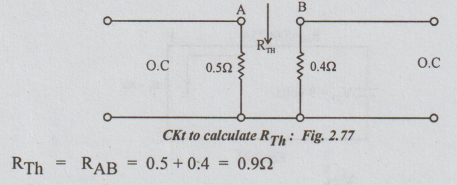
Step 3:

 [Note: The above problem can also be solved by other methods such as source conversion method and superposition principle.]

Example 5 Use Thevenin's theorem and find the current through (5+ j4) Ω impedance in the figure.

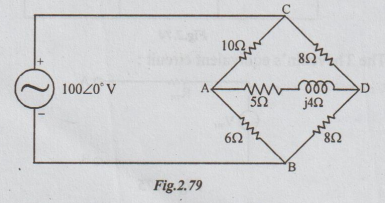
Solution: Step 1: To find VTh: Disconnect ZL = (5+j4) Ω

Step 2: To calculate ZTh = RTh: In the above circuit, kill the voltage source, by shorting C and D terminals.

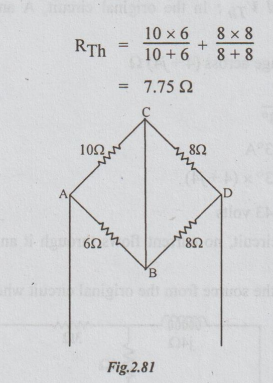
Step 3: Thevenin equivalent ckt

Example 6 Find the Thevenin's equivalent circuit for the network given in the figure.

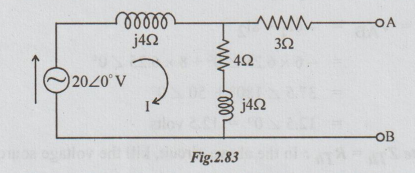
Solution: Step 1: To find VTh: In the original circuit, A and B terminals are shown open circuited.

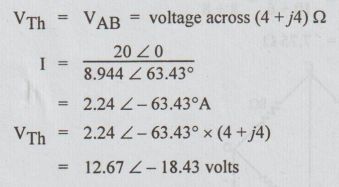
 [Note: As 3 Ω is in open circuit, no current flows through it and hence no voltage drop occurs across it.]

Step 2: To find ZTh: Kill the source from the original circuit where ZL is already removed.

Step 3: The Thevenin's equivalent circuit constant voltage generator circuit is

Example 7 Determine Thevenin's equivalent across the terminals A and B.

Solution: For clear understanding, let us re-draw the given circuit as shown below:

Step 1: To find VTh: For each loop, there are two resistors in series. By distribution of voltage formula,

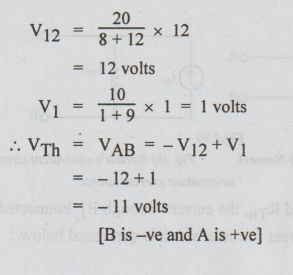
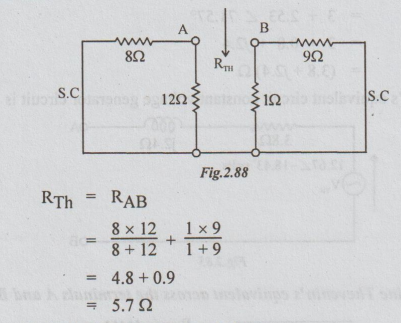
Step 2: To calculate RTh: Killing the source in the circuit shown in the fig. above, we get the following passive network.

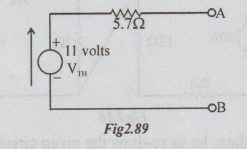
The Thevenin's equivalent circuit becomes as below: