Voltage and Current source transformation

SOURCE TRANSFORMATION

(VOLTAGE AND CURRENT SOURCE TRANSFORMATION)

For the mesh method of analysis, it is easier if the circuit has voltage sources. In the nodal analysis, it is easier if the circuit consists of current sources. In several cases, we may have to convert one type of source into another. This is for both A.C and D.C. circuits.

Figure.2.4 (a) shows an ideal voltage source in series with a resistance. Across the terminals A and B of the device, the voltage is e.

e = E- iR ... (1)

Figure.2.4 (b) shows a current source in parallel with a resistance. In this case, the current through R = I - i.

Voltage across R = e = (I - i) × R

= IR – iR ... (2)

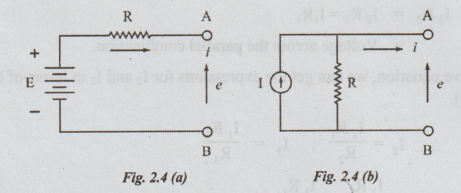
The equations (1) and (2) shown above are identical if E = IR.

Thus a current source in parallel with a resistance is equivalent to a voltage source in series with the same resistor, provided that the value of the voltage source is equal to the value of the current source, multiplied by the resistance. The conversion is valid in either direction and is shown in the figures 2.4 (a) and (b). The polarities of the sources are to be clearly noted in these examples.

In the above figures, for example, if E = 9 volts and R = 2 ohms, then I = 9 / 24.5 amperes and R remains same.

In the above current source, if I = 10 amperes and R = 3 ohms, then in the equivalent voltage source E = IR = 10 × 3 = 30 volts and R remains same i.e.,3 ohms.

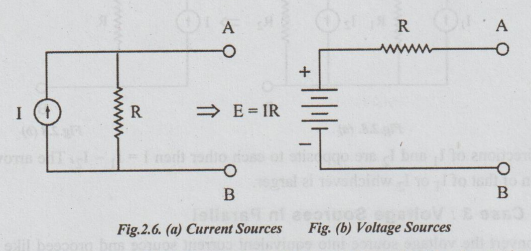
1. (a) Combination of Energy Sources

The following rules are followed to replace combination of sources by single equivalent source.

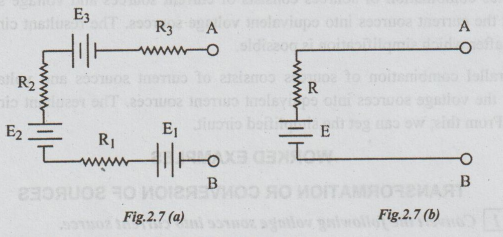
Case 1: Series Combination of Voltage Sources

Refer figure 2.7(a), where 3 voltage sources are in series between the terminals A and B. Its equivalent single source is shown in figure 2.7 (b) where E = E₁ + E₂ – E₃ and R = R₁ + R₂ + R₃.

(b) Case 2: Current Sources in Parallel

In figure 2.8 (a), current sources are shown in parallel. This can be replaced by a single current source, as shown in figure 2.8 (b).

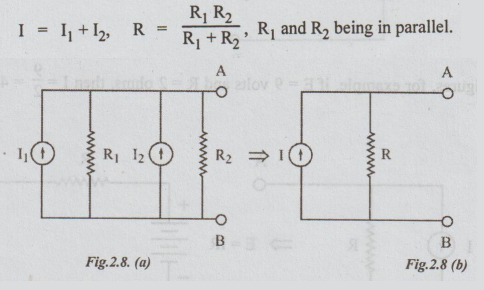
If the directions of I₁ and I₂ are opposite to each other then I = I₁ ~ I₂. The arrow for I will be in the direction of that of I₁ or 1₂ whichever is larger.

(c) Case 3: Voltage Sources in Parallel

First, convert the voltage source into equivalent current source and proceed like case 2 to get the equivalent current source. If necessary, the current source can be replaced by equivalent voltage source by using the formula.

 (d) Case 4: Current Sources in Series

Here, convert the current sources into equivalent voltage sources and simplify the combination as this comes under case 1.

Note:

1. Simplification of series connection of the sources is possible, if they are voltage sources.

2. Simplification of parallel connection of source is possible, if they are current sources.

3. If a series combination of sources consists of current sources and voltage sources, then first convert the current sources into equivalent voltage sources. The resultant circuit comes under case 1, after which simplification is possible. ww

4. If a parallel combination of sources consists of current sources and voltage sources, then convert the voltage sources into equivalent current sources. The resultant circuit comes under case 2. From this, we can get the simplified circuit.