(a) numerical single integration by Trapezoidal and simpson's 1rd / 3 Rules

(a) NUMERICAL SINGLE INTEGRATION BY TRAPEZOIDAL AND  SIMPSON'S 1^rd / 3 RULES

The process of evaluating a definite integral from a set of tabulated values of the integrand f (x) is called numerical integration. This process, when applied to a function of a single variable, is known as quadratic.

Newton-Cotes quadrature formula

This is known as Newton-Cotes quadrature formula. From this general formula, we deduce the following important quadrature rules by taking n = 1, 2, 3, ...

 

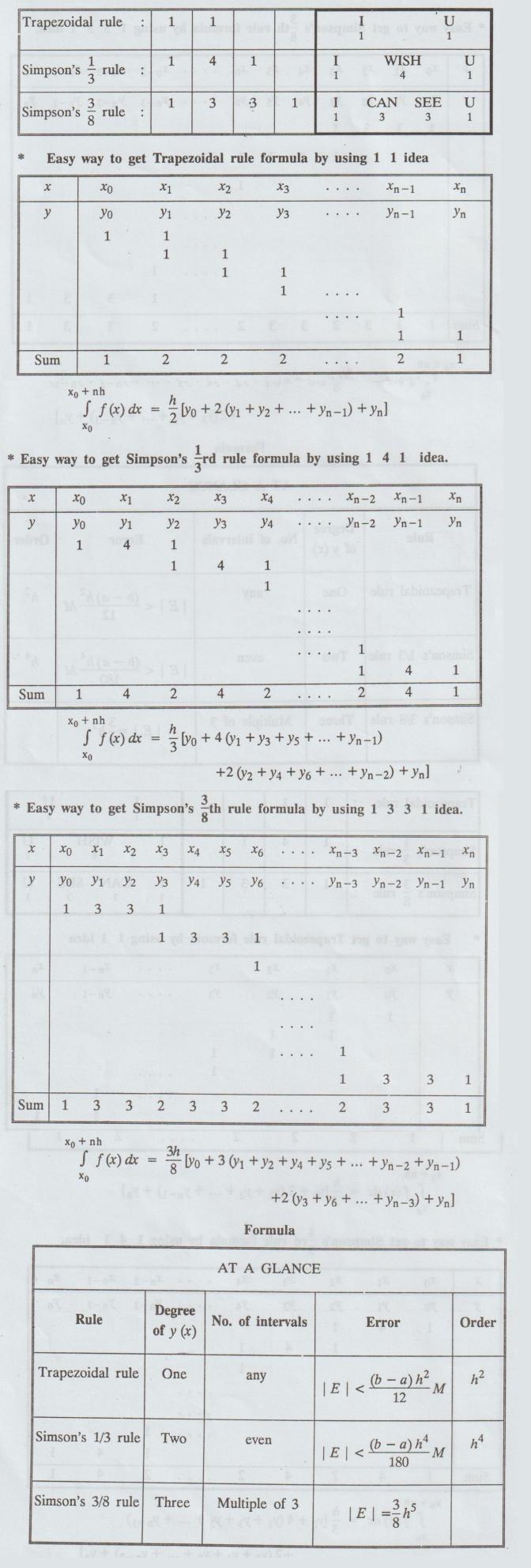
(i) Trapezoidal rule

Put n = 1 in (1) and take the curve through (xo, yo) and (x1,y1) as a straight line (i.e.,) a polynomial of first order, so that differences of order higher than first become zero, we get

(b) Simpson's 1/3^rd rule

Put n = 2 in (1) above take the curve through (xo, yo), (x1,y1) and (x2, y2) as a parabola (i.e.) a polynomial of second order, so that differences of order higher than second vanish, we get

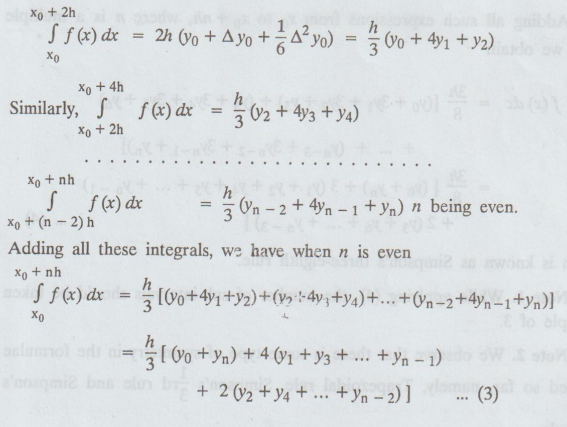
Simpson's one third rule = h/3{[Sum of the first and last ordinates]

+2[Sum of the remaining odd ordinates]

+4[Sum of the remaining even ordinates]}

Note 1. Though y₂ has suffix even, it is the third ordinate.

This is known as the Simpson's one-third rule or simply Simpson's rule and is most commonly used.

Note 2. While applying (3), the given interval must be divided into even number of equal sub-intervals, since we find the area of two strips at a time.

Simpson's three-eight rule

Put n = 3 in (1) above and take the curve through (x_i, y_i); i = 0, 1, 2, 3 as a polynomial of third order, so that differences above the third order vanish, we get

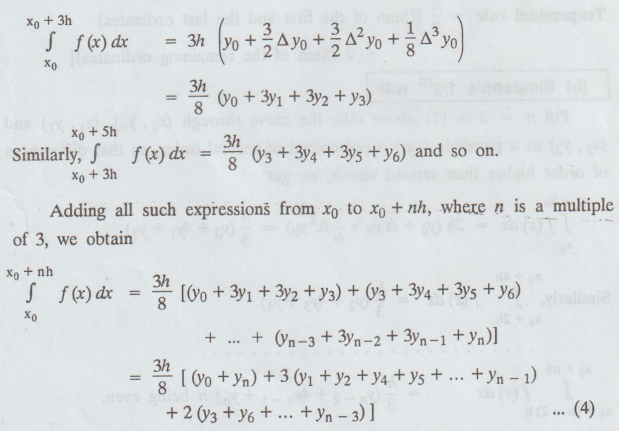
which is known as Simpson's three-eighth rule.

Note 1. While applying (4), the number of sub-intervals should be taken multiple of 3.

Note 2. We observe that there is some type of symmetry in the formulae derived so far, namely, Trapezoidal rule, Simpson's 3/ 3^rd rule and Simpson's 3/8th rule.

 

1. Dividing the range into 10 equal parts, find the value of  sin x dx by

 (i) Trapezoidal rule (ii) Simpson's rule.  [M.U. April 1996]

Solution :

Note: (1) Change degree mode to radian mode in your calculator.

(2) Fix 4 decimal places in your calculator.

2. By dividing the range into ten equal parts, evaluate  sin x dx by

Trapezoidal and Simpson's rule. Verify your answer with integration. [M.U. April, 96, A.U. M/J 2006] [A.U M/J 2013] [A.U A/M 2015 R-8] [A.U N/D 2012] [A.U A/M 2019 R-17]

Solution :

Note: (1) Change degree mode to radian mode in your calculator.

(2) Fix 4 decimal places in your calculator.

Range = π – 0 = π

Hence, h = π / 10

We tabulate below the values of y at different x's.

 

3. Evaluate: I 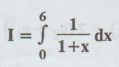by using

(i) Direct integration

(ii) Trapezoidal method

(iii) Simpson's 1/3rd rule

[A.U. N/D 2021 (R-17)] [A.U N/D 2011]

Solution :

 

5. Evaluate, 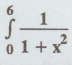 dx by (i) Trapezoidal rule (ii) Simpson's rule.

Also check up the results by actual integration.

[AU N/D 2004]

[A.U CBT N/D 2010, CBT A/M 2011, Tvli A/M 2011, N/D 2013] [A.U A/M 2015 R-13, R-8]

Solution:

Here, b - a = 6 – 0 = 6. Divide into 6 equal parts

h = 6/ 6 = 1. Hence, the table is

Conclusion: Here the value by trapezoidal rule is closer to the actual value than the value by Simpson's rule.

 

6. A rocket is launched from the ground. Its acceleration is registered during the first 80 seconds and is in the table below. Using trapezoidal rule an Simpson's 1/3 rule, find the velocity of the rocket at t = 80 sec.

Solution:

(i) Trapezoidal rule. Here h = 10.

 

7. Using Trapezoidal rule, evaluate  taking 8 intervals. [A.U. A/M 2004] [A.U M/J 2013]

Solution:

Here, y (x) = 1 / 1 + x²

Length of the interval = 2

So, we divide 8 equal intervals with h = 2 / 8 = 0.25

We form a table,

 

8. Evalute the integral 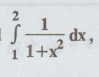using Trapezoidal rule with two sub intervals.

 

9. Using Trapezoidal Rule, evaluate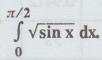 

Solution :

Note:

(1) Fix 4 decimal places in your calculator.

(2) Change degree mode to radian mode in your calculator.

 

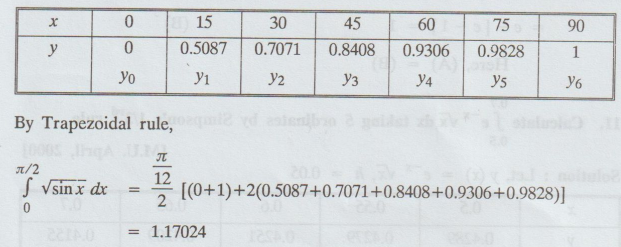
10. Using Simpson's one third rule evaluate 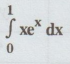 taking 4 intervals.

Compare your result with actual value. [M.U. Oct. 1998]

Solution :

 

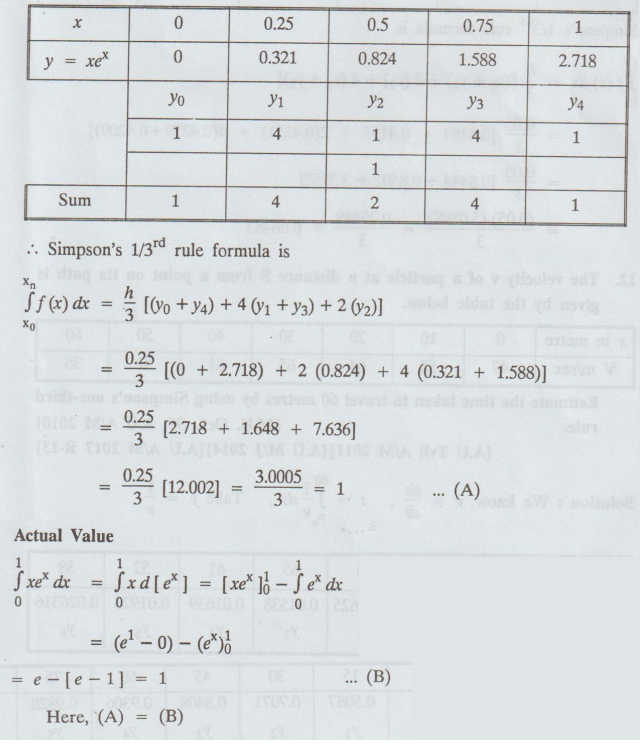
11. Calculate 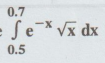 taking 5 ordinates by Simpson's 1/3rd rule.

Solution:

 

12. The velocity v of a particle at a distance S from a point on its path is given by the table below.

Estimate the time taken to travel 60 metres by using Simpson's one-third rule.

Tocar [M.U. Oct., 99, A.U A/M 2010]

[A.U Tvli A/M 2011] [A.U M/J 2014] [A.U A/M 2017 R-13]

Solution:

 

13. Find the value of log 2^1/3 from 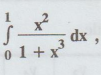 using Simpson’s one-third rule with h = 0.25

Solution:

14. Evalute , 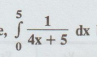 by Simpson's one-third rule and hence find the value of log_e 5 (n = 10).

Solution: ‘

Here, y (x) = 1 / 4x + 5

h = 5 – 0 / 10 = 1/2