(b) numerical double integrals by trapezoidal and simpson's 1/3rd Rules

(b) NUMERICAL DOUBLE INTEGRALS BY TRAPEZOIDAL AND SIMPSON'S 1/3^rd RULES

 

(a) Trapezoidal Rule for double integration

Consider the double integral

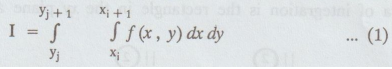
where x_{i + 1} = x; + h and y_{j + 1} = y_i + k

Apply trapezoidal rule repeatedly to get the value of I. As follows

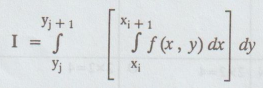
Apply trapezoidal rule to the inner integral, when y is a constant and x varies.

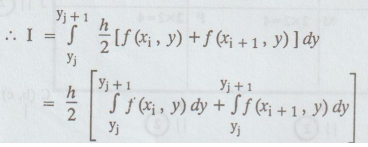
Now, apply trapezoidal rule to the two integrals. Here y varies and x1, Xi + 1 are constants.

Extension to general form of Trapezoidal rule JADIREMUM [using 1 1 idea]

Suppose, we want to evaluate 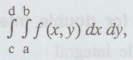, where a, b, c, d are constants. The area of integration is the rectangle in the xy plane as shown below.

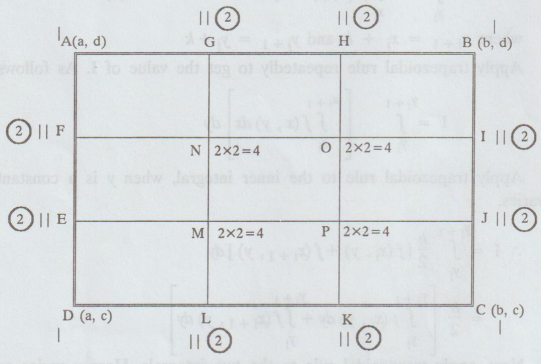
Divide the area of integration (rectangle ABCD) into meshes by dividing AB into 3 equal parts (in general into m equal parts) each part length being h, and AD into 3 equal parts, (in general n equal parts) each part length being k.

Now, the integral over the whole rectangle is equal to sum of the integrals over each mesh. So, extending the formula given by (3),

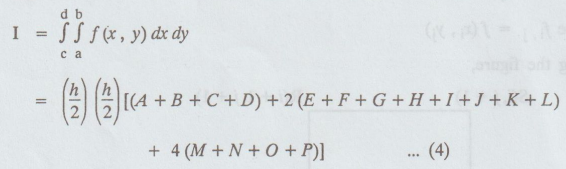
I = hk / 4 [(Sum of values of ƒ at the four corners)

+ 2 (Sum of the values of ƒ at the remaining nodes on the boundary) + 4 (Sum of the values of the values of ƒ at the interior nodes)] ... (5)

 

 (b) Simpson's rule for double integration

I = hk / 9  [(Sum of the values of ƒ at the four corners)

+ 2 (Sum of the values of f at the odd positions on the boundary except the corners)

+ 4 (Sum of the values of ƒ at the even positions on the boundary)

+ {4 (Sum of the values of ƒ at odd positions)

+ 8 (Sum of the values of f at even positions) on the odd rows

of the matrix except boundary rows }

+ {8 (Sum of the values of f at the odd positions)

+ 16 (Sum of the values of ƒ at the even positions) on the even rows of the matrix}]

 

1. Evaluate 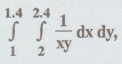 using Trapezoidal and Simpson's rule.Verify your result by actual integration.

[A.U CBT A/M 2011] [A.U CBT N/D 2011, N/D M/J 2013] [A.U N/D 2021 R-17]

Solution :

Divide the range of x and y into 4 equal parts.

H = 2.42 – 4 / 4 = 0.1 and k = 1.4 – 4 / 4 = 0.1

Get the values of f (x, y) = 1/xy at nodal points.

Case (1) By Trapezoidal rule, we get

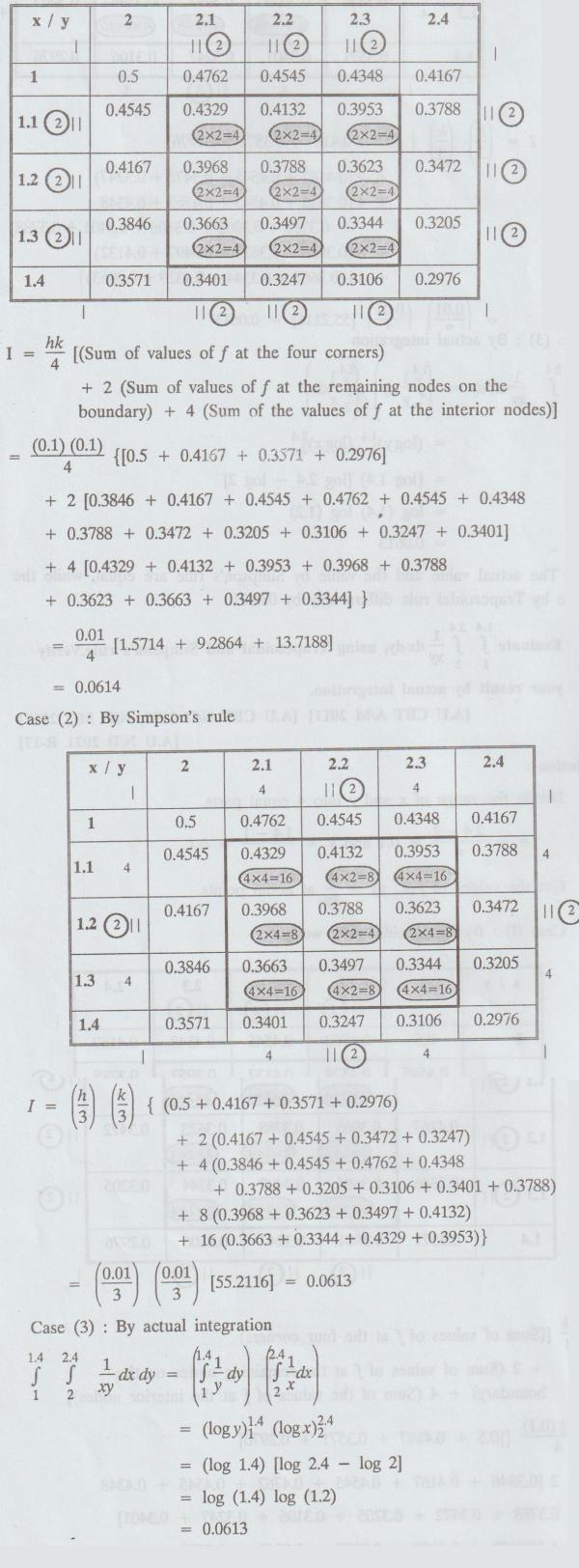
The actual value and the value by Simpson's rule are equal, while the value by Trapezoidal rule differs only by 0.0001.

 

2. Evaluat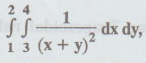e  taking h= k = 0.5 by both Trapezoidal rule and Simpson's rule.

 [A.U N/D 2020 R-17 NM] [A.U. A/M 2021 R-17 NM]

Solution:

 

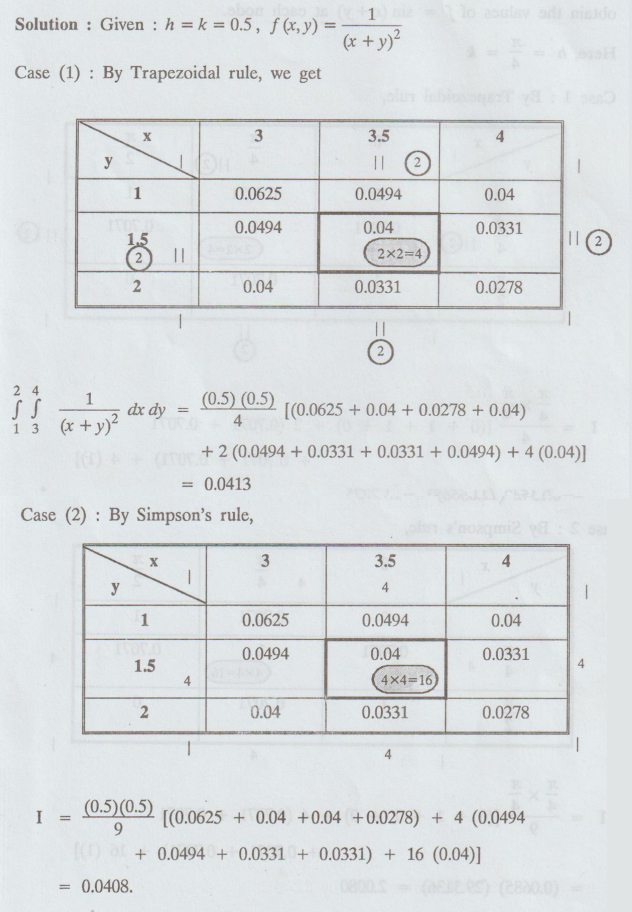
3. Evaluate, 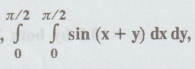 sin (x + y) dx dy, by using Trapezoidal rule.nava

Simpson's rule and also by actual integration.'

Solution: Divide the range on x and y direction into equal parts and obtain the values of f sin (x + y) at each node.

Here, h = π / 4 = k

Case 1: By Trapezoidal rule,

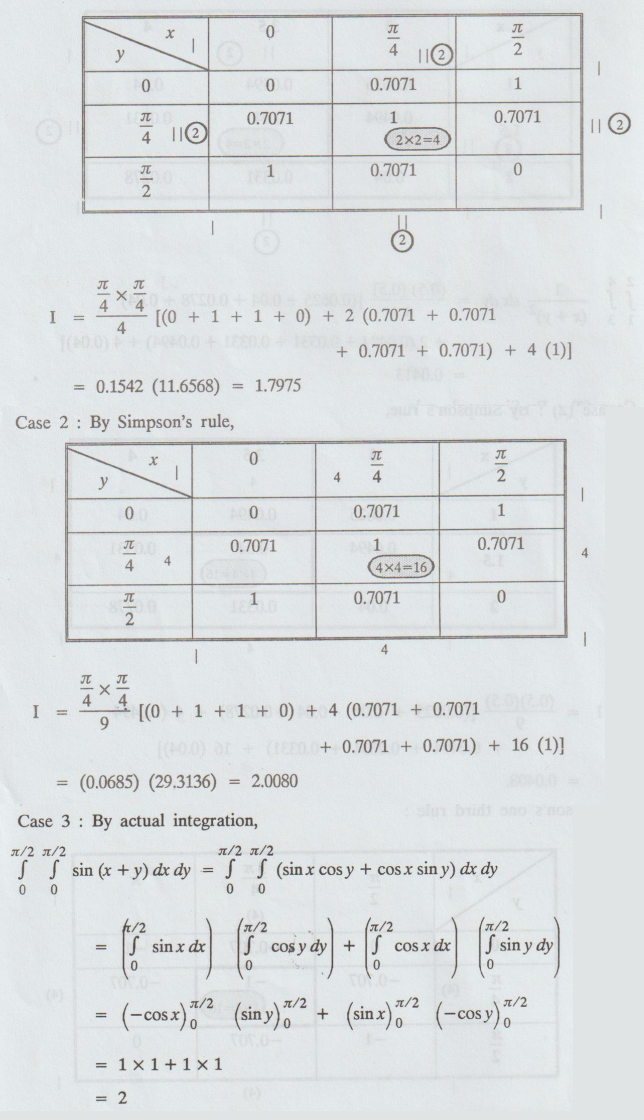
The value got by Simpson's rule differs from the exact value only by 0.008, while the error in the Trapezoidal rule is 0.2125.

 

4. Evaluate 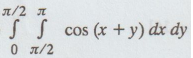 by using Trapezoidal rule by taking h = k = π / 4 [A.U M/J 2016 R13 (NM)] [A.U N/D 2020 R-17] [A.U A/M 2021 R-17]

Solution:

 

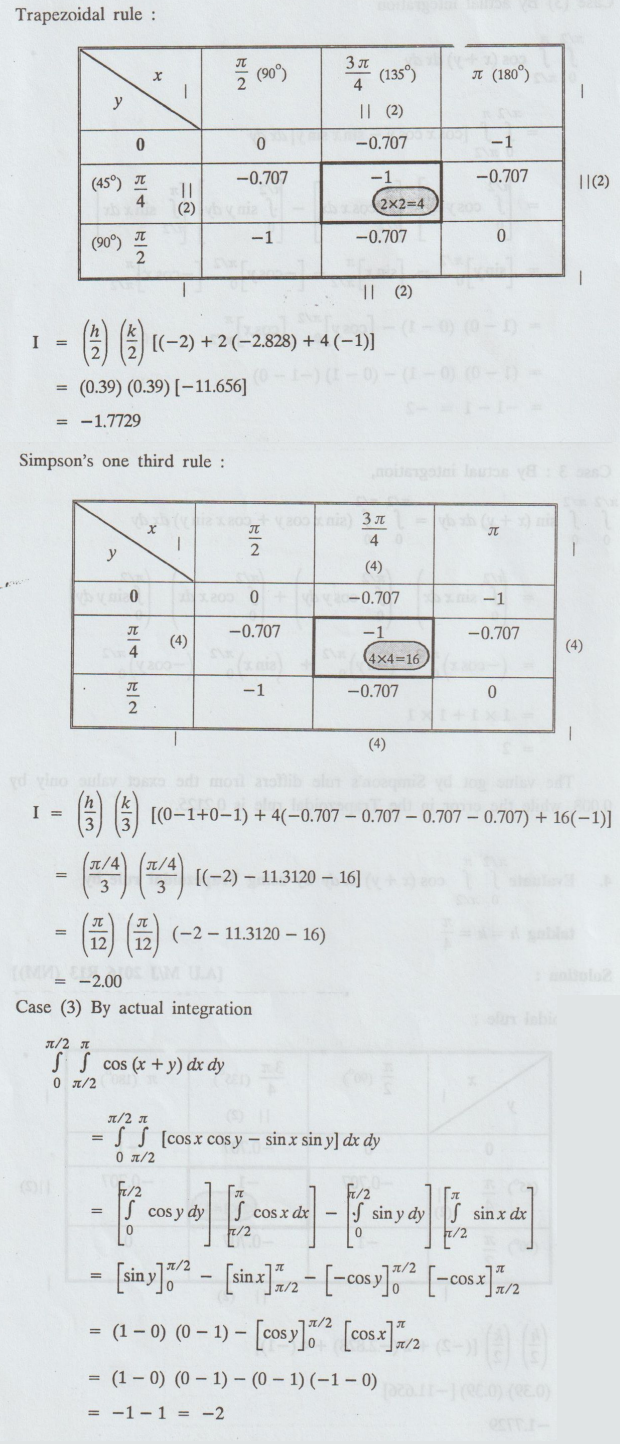
5. Evaluate sin (9x + y) dx dy by Simpson's 1/3rd rule and Trapezoidal rule with h = 0.25 and k = 0.5

[A.U N/D 2016 R13 (SNM)]

Solution :

 f(x, y) = sin (9x + y), h = 0.25, k = 0.5

By Trapezoidal rule

 

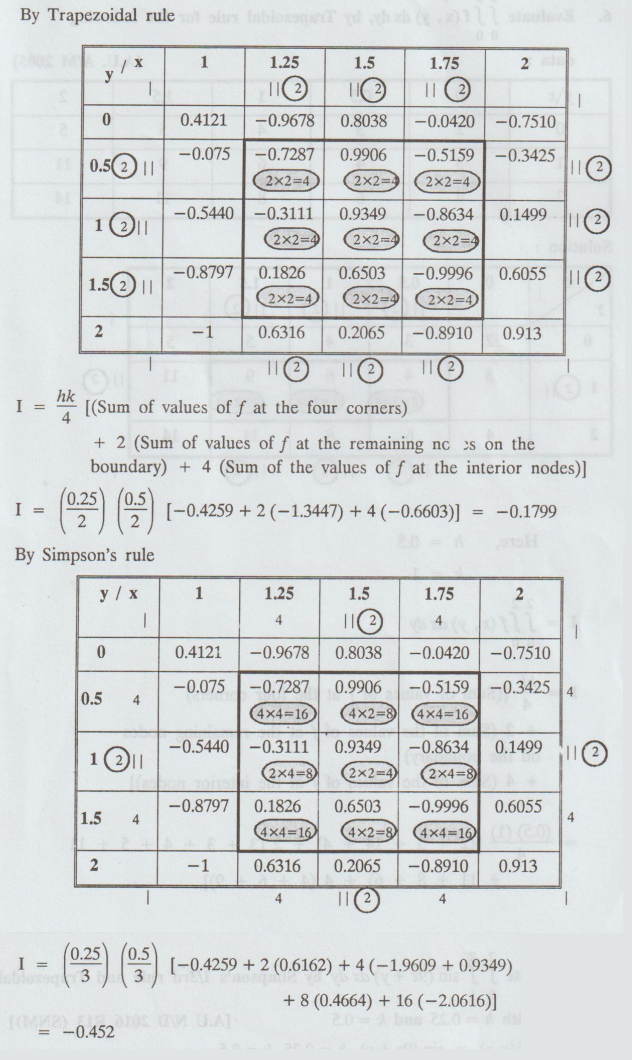
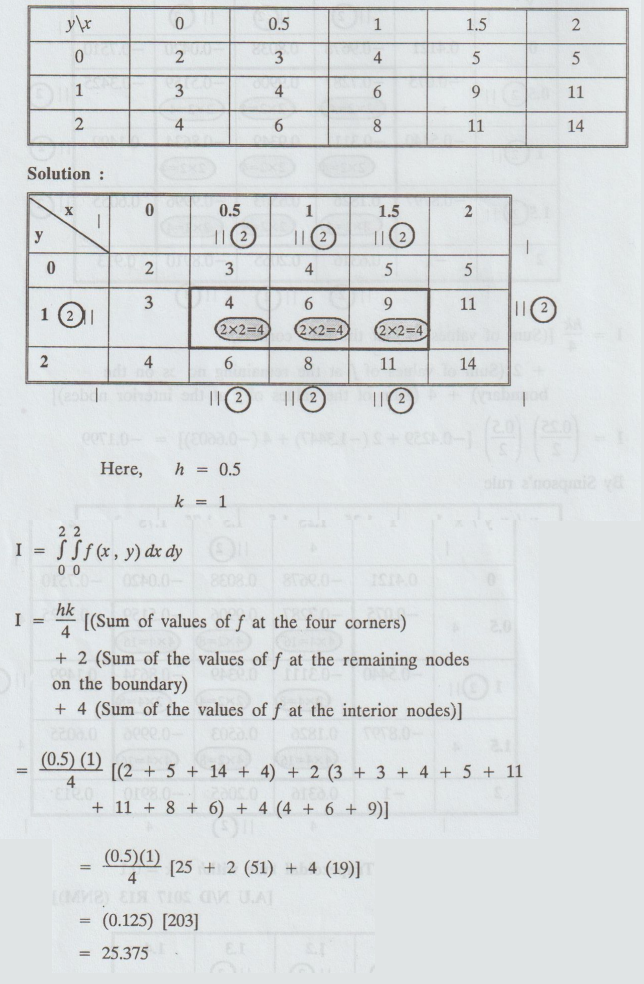
6. Evaluate 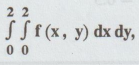 by Trapezoidal rule for the following data :

 

8. Evaluate 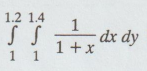 by Trapezoidal rule with h = k = 0.1

Solution :

 

9. Evaluate 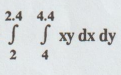 by Trapezoidal rule taking h = k = 0.1

Solution :

 

10. Evaluate 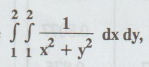 numerically with h = 0.2 along x-direction and k = 0.25 along y-direction.

Solution :

 

11. Evaluate numerically 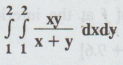 with h = k = 0.25

Solution :

 

12. Using Simpson’s 1/3 rule, evaluate 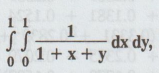 taking h = k = 0.5

Solution :

 

13. The function f(x,y) is defined by the following table. Compute 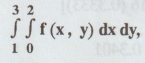 using Simpson’s rule in both direction.

Solution :

 

14. Using Simpson’s rule evaluate 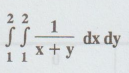 by dividing the interval (1,2) into two equal sub intervals.

Solution :

 

15. Evaluate 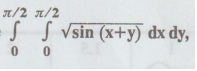by numerical double intergration using Simpson’s rule or Trapezoidal rule with h = k = π/4

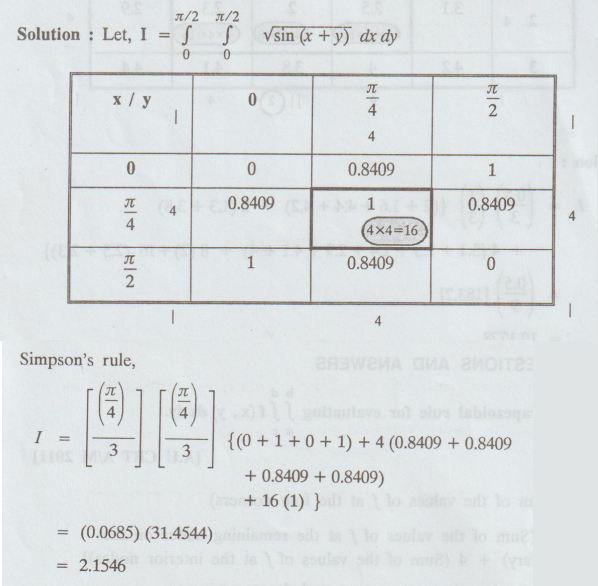
Solution :

 

16. Evaluate 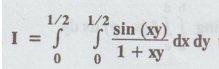 using Simpson’s rule with h = k = ¼.

Solution :