Anna university solved problems

ANNA UNIVERSITY SOLVED PROBLEMS

Carrier concentration in an intrinsic semiconductor

Problem 3.1

Find the resistance of an intrinsic germanium rod 1 cm long, 1 mm wide and 1 mm thick at 300 K.

For germanium n_i = 2.5 × 10¹⁹ m^-3

µ_e = 0.39 m² V^-1s^-1

µ_h = 0.19 m² V^-1s^-1 at 300 K    [A.U. Dec. 2014]

Given data

Intrinsic carrier concentration n_i = 2.5 × 10¹⁹ m^-3

Electron mobility µ_e = 0.39 m² V^-1s^-1

Hole mobility μ_h = 0.19 m² V^-1s^-1

1 = length of the rod = 1 cm = 1 × 10^{- 2}m

A = Area of cross-section (width × thickness)

A = (1 × 10^-3) (1 × 10^-3)

Solution

Electrical conductivity of an intrinsic semiconductor

σ = n_ie (μ_e + μ_h)

Substituting given values, we have

σ = 2.5 × 10¹⁹ × 1.6 × 10^-19 × (0.39 + 0.19)

σ = 2.32 Ω^-1 m^-1

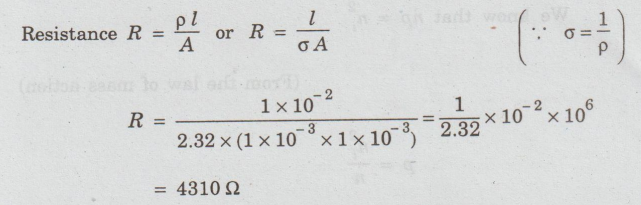
Resistance of germanium = 4310 Ω.

 

Extrinsic semiconductor

Problem 3.2

Find the concentration of holes and electrons in n-type silicon at 300 k, if the conductivity is 3 × 10⁴ ohm^-1 m^-1. Also find these values for p – type silicon.

Given data

For silicon at 300 K, n_i = 1.5 × 10¹⁶ m^-3

µ_e = 1300 × 10^-4 m² V^-1 s^-1

µ_h = 500 × 10^-4 m² V^-1 s^-1

Solution

(a) Concentration in n-type silicon

 (b) Concentration in p-type silicon

 

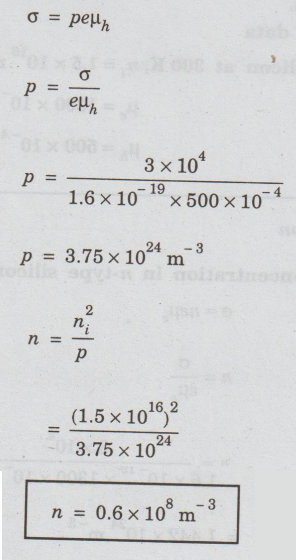
Problem 3.3

A silicon material is uniformly doped with phosphorus atoms at a concentration of 2 × 10¹⁹ m^-3. The mobilities of holes and electrons are 0.05 and 0.12 m 0.05 and 0.12 m² V^-1 s^-1 respectively, n_i = 1.5 × 10¹⁶m^-3. Find the electron and hole concentrations and electrical conductivity.  (A.U. June 2014)

Solution

 

Problem 3.4

Find the hole and electron concentrations in a p-type semiconductor, if the acceptor density is 10²⁰ atoms/m³ and the intrinsic concentration is 2.5 × 10¹⁹ per m³ at 300 K.  (A.U. May 2016)

Solution

In a p-type semiconductor, the hole concentration is equal to the acceptor density.

 

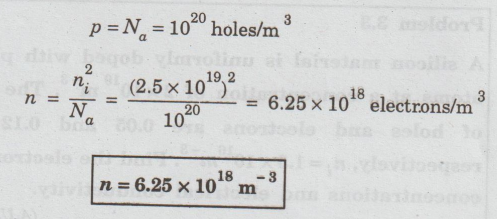
Hall effect

Problem 3.5

The Hall coefficient of a specimen of a doped silicon is found to be 3.66 × 10^-4 m³/C. The resistivity of the specimen is 8.93 × 10^-3 Ωm. Find the mobility and density of the charge carriers. (A.U.April 2015)

Given data

Hall coefficient of the specimen R_H = 3.66 × 10^-4 m³/C

Resistivity of the specimen ρ = 8.93 × 10^-3 Ωm

Mobility of the carrier μh = ?

Density of charge carriers nh = ?

Solution

We know that density of charge carriers

n_h = 1 / R_He

Substituting the given values, we have

n_h =  1 / 3.66 × 10^-4 × 1.610 × 10^-19

n_h =  1.708 × 10²² m^-3

µ_h = 1 / ρ n_he

µ_e = R_H / ρ

µ_h = 3.66 × 10^-4 / 8.93 × 10^-3

µ_h = 0.041 m² V^-1 s^-1

 

Problem 3.6

Find the Hall coefficient and electron mobility of germanium for a given sample (length 1 cm, breadth 5 mm, thickness 1 mm). A current of 5 milliampere flows from a 1.35 volt supply and develops a Hall voltage of 20 millivolt across the specimen in a magnetic field of 0.45 Wb/m². (A.U. May 2013)

Given data

Current through the specimen I = 5 mA or 5 × 10^-3 A

Voltage across the specimen V = 1.35 V

Length of the sample L = 1 cm or 1 × 10^-2 m

Breadth of the sample b = 5 mm or 5 × 10^-3 m

Thickness of the sample t = 1 mm or 1 × 10^-3 m

Hall voltage V_y = 20 × 10^-3 V

Magnetic field H = 0.45 Wb/m²

Solution :

We know that resistivity ρ = Ra/l

where R→ Resistance of the specimen

Hall coefficient

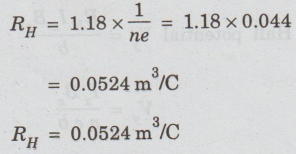
Electron mobility

 

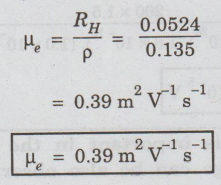
Problem 3.7

A copper strip 2.0 cm wide and 1.0 mm thick is placed in a magnetic field with B = 1.5 weber/m perpendicular to the strip. Suppose a current of 200 A is set up in the strip. What Hall potential difference would appear across the strip?

Given N = 8.4 × 10²⁸ electrons /m³. (A.U. May 2015)

Given data

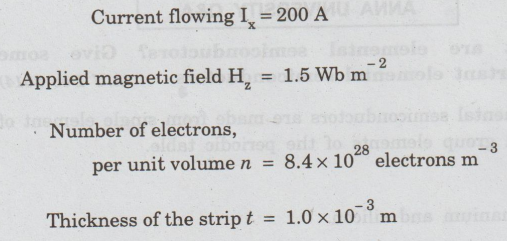
Solution :

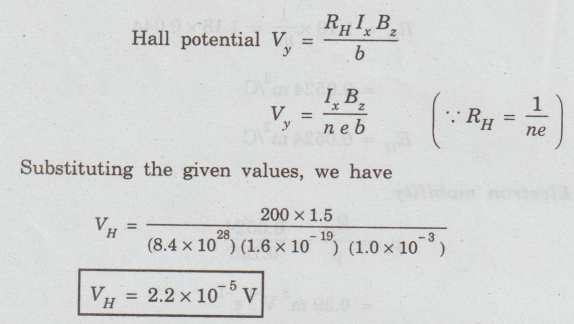
Note: This problem is important in the sense that it shows that Hall voltage can be also observed in metals besides semiconductor.

In semiconductors, Hall voltage is comparatively much larger; it is of the order of milli-volts as compared to the order of micro-volts in metals.

Moreover, to observe Hall voltage in metals, current of the order of amperes is needed when compared to the order of milliamperes as in the case of semiconductors.