Statistics and Numerical Methods: Unit IV: Interpolation, numerical differentiation and numerical integration

Newton's divided difference interpolations

Solved Example Problems

Home | Department: EEE Department | Ist Year | Subject: Statistics and Numerical Methods |

<< Previous

Next >>

Let, y = f(x) take values f (x0), f(x1) ... f (xn) corresponding to the arguments x0, x1, ... Xn

NEWTON'S DIVIDED DIFFERENCE INTERPOLATIONS

Let, y = f(x) take values f (x₀), f(x₁) ... f (x_n) corresponding to the arguments x₀, x₁, ... X_n

By definition,

1. Using Newton's divided difference formula, find u(3) given u(1) = -26, ad u(2) = 12, u(4) = 256, u(6) = 844.

[A.U. April/May 2004]

Solution:

We form the divided difference table, since the intervals are unequal

2. Find f (x) as a polynomial in x for the following data by Newton's divided difference formula

3. Finf f(8) by Newton’s divided difference formula for the data :

4. Find the function f(x) from the following table using Newton’s divided difference formula :

Solution :

We from the divided difference table, since the intervals are unequal

5. Given values

Evalute f(9) using Newton’s divided difference formula

Solution :

The divided difference table is as follows :

6. Given the data :

Find the cubic function of x

Solution :

The divided difference table is as follows :

7. Using Newton’s divided difference formula, find f (x) and f (6) from the following data :

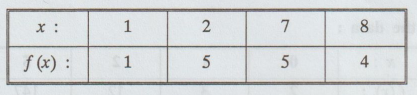
Solution :

The divided difference table is

8. Using Newton’s divided difference formula, find f (5) from the following data :

Solution :

The divided difference table is

9. Given the following data find y (6), y (5) and the maximum value of y.

Solution : since the arguments are not equally spaced, we will use Newton’s divided difference formula

The divided Difference Table is

y(x) is maximum if y’ (x) = 0 3x² + 4x + 3 = 0. But the roots are imaginary. Therefore, there is no extremum value in the range. In fact it is an increasing curve.

10. Find the fourth degree curve y = f(x) passing through points (2,3), (4,43), (5,138), (7,778) and (8, 1515) using Newton’s divided difference formula.

Solution :

Statistics and Numerical Methods: Unit IV: Interpolation, numerical differentiation and numerical integration : Tag: : Solved Example Problems - Newton's divided difference interpolations

Home | Department: EEE Department | Ist Year | Subject: Statistics and Numerical Methods |

<< Previous

Next >>

Statistics and Numerical Methods: Unit IV: Interpolation, numerical differentiation and numerical integration

Interpolation, numerical differentiation and numerical integration

Lagrange's Interpolation - Solved Example Problems

Lagrange's Inverse interpolation - Solved Example Problems

Short Questions and Answers - Lagrange's Interpolation

Exercise 4.1 [Lagrange's Interpolation] - Solved Example Problems

Newton's divided difference interpolations - Solved Example Problems

Short Questions and Answers - Newton's Divided Differences interpolation

Exercise 4.2 [Newton's Divided Differences interpolation] - Solved Example Problems

Newton's forward and backward difference interpolation - Solved Example Problems

Short Questions and Answers - Newton forward and backward difference

Exercise 4.3 - [Newton forward and backward difference W 1- eros MA U.A][010S (MU.A] formula] - Solved Example Problems

Approximation of derivatives using interpolation polynomials - Solved Example Problems

Short Questions and Answers - Approximation of derivatives using interpolation polynomials

Exercise 4.4 [Approximation of derivatives using interpolation polynomials] - Solved Example Problems

(a) numerical single integration by Trapezoidal and simpson's 1rd / 3 Rules - Solved Example Problems

Under Subject

Statistics and Numerical Methods

MA3251 2nd Semester 2021 Regulation M2 Engineering Mathematics 2 | 2nd Semester Common to all Dept 2021 Regulation

Related Subjects

Professional English II

HS3251 2nd Semester 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation

Statistics and Numerical Methods

MA3251 2nd Semester 2021 Regulation M2 Engineering Mathematics 2 | 2nd Semester Common to all Dept 2021 Regulation

Engineering Graphics

GE3251 eg 2nd semester | 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation

Physics for Electrical Engineering

PH3202 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation

Basic Civil and Mechanical Engineering

BE3255 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation

Electric Circuit Analysis

EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation

Physics for Electronics Engineering

PH3254 - Physics II - 2nd Semester - ECE Department - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation

Electrical and Instrumentation Engineering

BE3254 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation

Circuit Analysis

EC3251 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation

Materials Science

PH3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation

Basic Electrical and Electronics Engineering

BE3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation

Physics for Civil Engineering

PH3201 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation

Basic Electrical, Electronics and Instrumentation Engineering

BE3252 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation

Physics for Information Science

PH3256 2nd Semester CSE Dept | 2021 Regulation | 2nd Semester CSE Dept 2021 Regulation

Basic Electrical and Electronics Engineering

BE3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation

Programming in C

CS3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation