Short Questions and Answers

SHORT QUESTIONS AND ANSWERS

1. State Lagrange's interpolation formula. [A.U CBT N/D 2010] [M.U. Oct., 2000, A.U. April 2000, Tvli M/J 2010, CBT A/M 2011] [A.U N/D 2011] [A.U N/D 2014]

Solution:

Let y = f (x) be a function which takes the values y₀, y₁, ... y_n corresponding to x = x₀,x₁.... x

Then, Lagrange's interpolation formula is

2. What is the Lagrange's formula to find y, if three sets of values (xo, yo), (x1, y1) and (x2, y2) are given.

Solution :

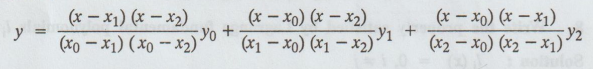
3. What is the assumption we make when Lagrange's formula is used?  [M.U. April, 2001]

Solution:

Lagrange's interpolation formula can be used whether the values of x, the independent variable are equally spaced or not whether the difference of y become smaller or not.

4. What advantage has Lagrange's formula over Newton ?

Lagrange's method

1. We can apply both equally and unequally spaced arguments.

2. Can be used to interpolate any where in the range.

Newton's method

1. The arguments are equally spaced.

2. Newton's forward formula is suitable to interpolate near the beginning. Newton's backward formula is suitable to interpolate ained) worl ton ai noitomuto near end of the value.

5. What is the disadvantage in practice in applying Lagrange's interpolation [00 formula?

Solution:

Though Lagrange's formula is simple and easy to remember, its application in calculation is not speed. It requires close attention to sign and there is always a chance of committing some error due to a number of positive and negative signs in the numerator and the denominator.

6. What is 'inverse interpolation"? [A.U Tvli N/D 2010, A.U. N/D 2007]

Solution :

Suppose, we are given a table values of x and y direct interpolation is the process of finding the values of y corresponding to a value of x, not present in the table. Inverse interpolation is the process of finding the values of x corresponding to a value of y, not present in the table.

7. Give the inverse of Lagrange's interpolation formula.

Solution :

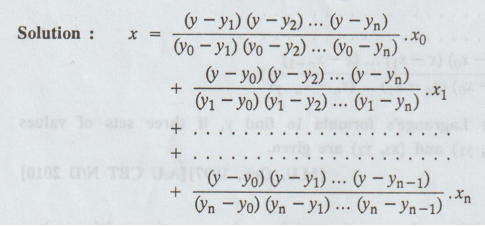
8. Write the property satisfied by Lagrange fundamental polynomials ; (x)

Solution:

li (x) = 0, i ≠ j

= 1, i = j

9. Write the expression for the bound on the error in Lagrange's interpolation.

Solution:

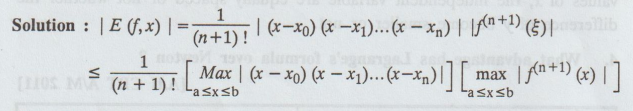
10. What do you meant by interpolation?  (or) Explain briefly interpolation.  [A.U N/D 2006, A.U. CBT A/M 2011, CBT N/D 2011]

Solution:

The process of finding the value of a function inside the given range is called Interpolation.

Interpolating function: Let a set of tabular values of a function y = f (x), where the explicit nature of the function is not known, then f(x) is replaced by a simplest function ϕ (x), such that f (x) and ϕ (x) agree with the set of tabulated points Any other value may be calculated from (x). This function (x) is known as an interpolating function.

11. Can you use Lagrange's interpolation formula, when the intervals are equal?

Solution: Yes

12. Write the Lagrange's fundamental polynomial Lo (x) and L1 (x) that satisfy the condition Lo (x) + L1 (x) = 1 for the [x0, f (x0)] [x1, f(x1)]

Solution:

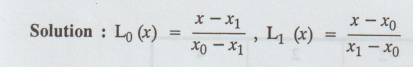
13. Using Lagrange’s formula, find the polynomial to the given data:

14. Given f(2) = 5, f (2.5)= 5.5 find the linear interpolating polynomial using Lagrange interpolation. [A.U N/D 2019 (R13)]

Solution :