Short Questions and Answers

SHORT QUESTIONS AND ANSWERS

 

1. Why is Trapezoidal rule so called? [M.U. Oct., 97] [A.U Tvli M/J 2010]

Solution

Trapezoidal rule is so called because it approximates the integral by the sum of n Trapezoids.

 

2. How the accuracy can be increased in Trapezoidal rule of evaluating a given definite integral ? 10 81 [M.U, Oct. 97]

Solution:

If the number of points of the base segment b-a, (the range of integration) is increased, a better approximation to the area given by the definite integral will be obtained.

 

3. State the Trapezoidal rule to evaluate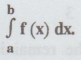 

 [M.U, April 96]

Solution :

Let DC be the curve y = f (x) and DA, CB be the terminal ordinates. Let OA = a and OB = b.

Then, AB = OB – OA = b - a

Divide AB into n equal parts A A₁, A A₂,... A_{n - 1} B

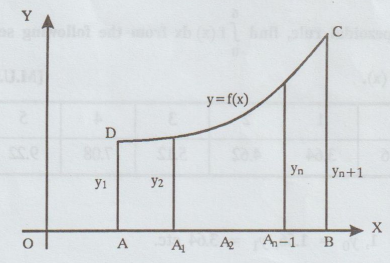
so that each part = b – a = h (say) Draw the ordinates through A,

A₁, ... A_{n - 1}, B and let the 1 be called. ! y₁, y₂, y_n , y_n+1 respectively.

Then, 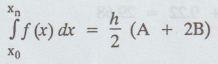 approximately ... (1),

where A = y₁ + y_{n +1} = sum of the first and the last ordinates and B = y₂ + y₃ + ... + y_n = sum of the remaining ordinates (1) is known as trapezoidal rule.

 

 

6. State Simpson's rule. (or)

State Simpson's one-third rule. (or)

 [A.U N/D 2009]

Write down the formula for Simpson's one-third rule.

[M.U, Oct. 1996] [A.U M/J 2013, N/D 2011]

Solution: Let DC be the curve of y = f (x) and DA, CB be the terminal ordinates. Let OA = a and OB = b. Divide AB into even number (say 2n) of equal parts, equal to h. Let x₁, x₂,… x_2n+1  be the abcissa of the points  A, A₁, … B and y₁,y₂,… y_2n+1 corresponding ordinates. Then,

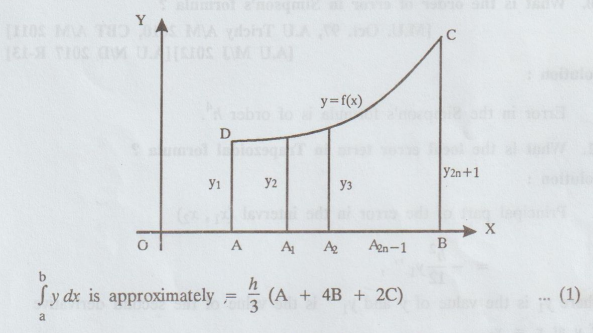
where A = y₁ + y_2n+1 = sum of the first and the last ordinates.

B = y₂ + y₄ + … y_2n  = sum of the even ornates and

C = y₃ + y₅ + … + y_2n-1 = sum of the remaining

ordinates (1) is known as Simpson's rule or Simpson's one-third rule.

 

7. When does Simpson's rule give exact result?

[M.U. Oct., 95] [A.U. M/J 2006] [A.U CBT A/M 2011]

Solution: Simpson's rule will give exact result, if the entire curve y = f (x) is itself a parabola.

 

8. What is the general Newton-Cotes quadrature formula ? How is the Trapezoidal rule its special case ?

Solution: The general Newton-Cotes quadrature formula is

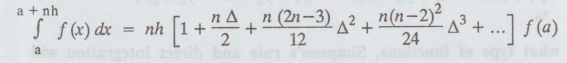
This is also known as the general Gauss-Lagender integration formula. Putting n 1 and omitting second and higher differences in the above, we get

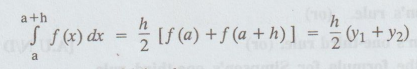
which is the Trapezoidal rule.

 

9.  What is the order of error in Trapezoidal formula.

 [A.U CBT N/D 2010, Trichy A/M 2010, CBT A/M 2011] [A.U N/D 2017 R-13]

Solution :

Error in the Trapezoidal formula is of order h².

 

10. What is the order of error in Simpson's formula ?

 [M.U. Oct. 97, A.U Trichy A/M 2010, CBT A/M 2011] [A.U M/J 2012] [A.U N/D 2017 R-13]

Solution :

Error in the Simpson's formula is of order h⁴.

 

11. What is the local error term in Trapezoidal formula ?

Solution :

Principal part of the error in the interval (x₁, x₂)

= - h² / 12^y1

where y1 is the value of y and y1 "is the value of the second derivative of y at x = x₁.

 

12. State the local error term in Simpson's one third rule. [A.U N/D 2014 NM]

Solution :

Principal part of the error in the interval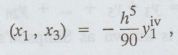 

where y₁ is the value of y and y₁^iv is the value of the fourth derivative of y at x = x1

 

 

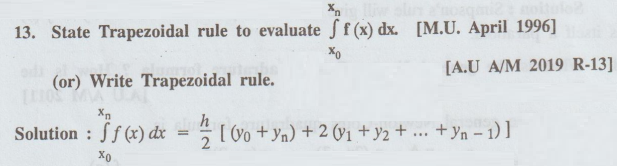
14. For what type of functions, Simpson's rule and direct integration will sl give the same result?

[M.U. Oct. 1998]

Solution:

Simpson's rule will give exact result, if the entire curve y = f (x) is itself a parabola.

 

15. Error in Simpson's rule is of order ……

Solution: h⁴

 

16. Six sets of values of x and y are given (x's being equally spaced). Write the formula to get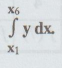 

 

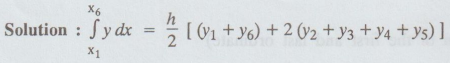
17. Which one is more reliable, Simpson's rule or Trapezoidal rule ?

 Solution: Simpson's rule.

 

18. What are the errors in Trapezoidal and Simpson's rules of numerical integration ? [A.U. A/M 2003] [A.U M/J 2016 R13]

Solution:

 

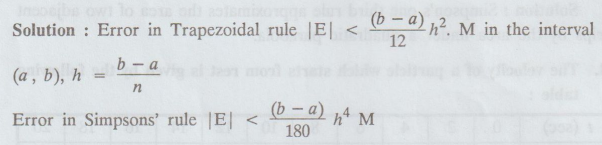
19. State True or false.

Whenever Trapezoidal rule is applicable Simpson's rule can be applied.

Solution: False.

 

20. Using Trapezoidal rule, evaluate  sin x dx by dividing the range into 6 equal parts.

 

21. Write down the Trapezoidal rule to evaluate 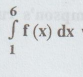dx with h = 0.5. [A.U A/M 2005]

Solution: Here, f (x) = h = 0.5

 

22. What approximation is used in deriving Simpson's rule of integration ?

Solution:

Simpson's one third rule approximates the area of two adjacent strips by the area under a quadratic parabola.

 

23. The velocity of a particle which starts from rest is given by the following table :

 

24. From the following table find the area bounded by the curve and the x-axis from x = 2 to x = 7.

Solution: Here, h = 1 and only 6 ordinates are given.

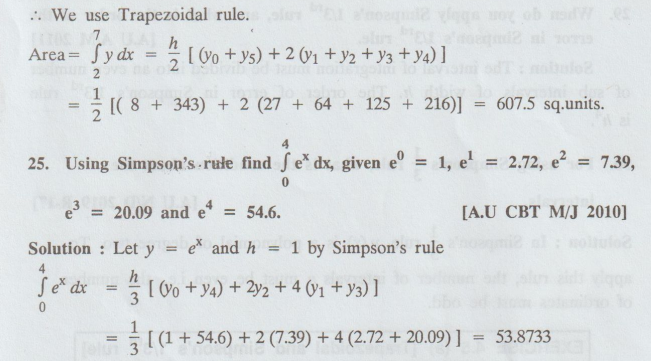
26. State the Romberg's integration formula with h₁ and h₂.

Further, obtain the formula, when h₁ = h, and h₂ = h/2

 

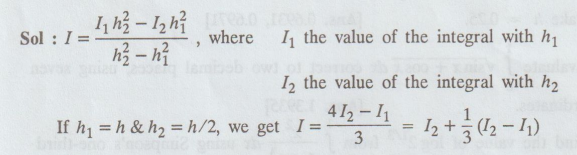
27. Compare Trapezoidal rule and Simpson's 1/3 rule for evaluating numerical integration.

 

28. State the basic principle for deriving simpson's 1/3^rd rule.

The curve passing through three consecutive points is replaced by a parabola.

 

29. When do you apply Simpson's 1/3rd rule, and what is the order of the error in Simpson's 1/3rd rule. [A.U A/M 2011]

Solution:

The interval of integration must be divided into an even number of sub intervals of width h. The order of error in Simpson's 1/3rd rule is h⁴.

 

30. For using Simpson's 1 / 3 rule, what is the condition about the intervals.

[A.U N/D 2019 R-17]

Solution:

In Simpson's 1 / 3 rule, y (x) is a polynomial of degree two. To apply this rule, the number of intervals n must be even i.e., the number of ordinates must be odd.