Various Representation of Flip-Flops

Various Representation of Flip-Flops

1. Characteristic Equations of Flip-Flops

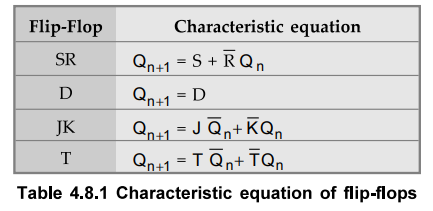
• The characteristic equations for various flip-flops are summarized in Table 4.8.1.

2. Flip-Flops as Finite State Machines

• In a sequential logic circuit Finite State Machine (FSM) the value of all the memory elements at a given time define the state of that circuit at that time. In FSM, the functional behaviour of the circuit is represented using the state transition diagram.

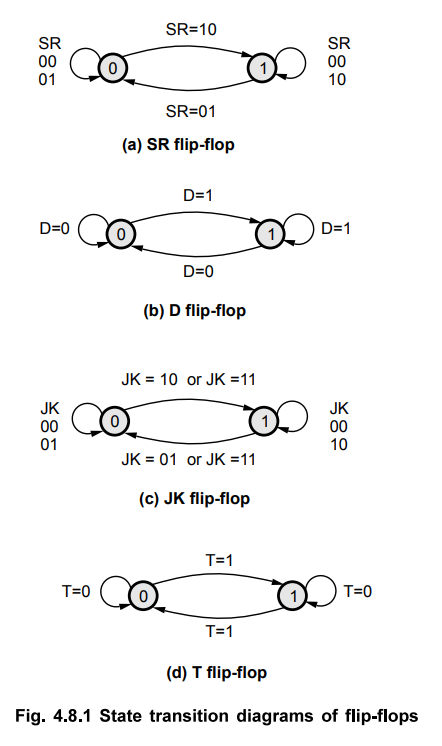
 Let us the representation of flip-flops in their state transition diagrams.

• The Fig. 4.8.1 shows the state transition diagram for all flip-flops. Here, the 0 and the 1 in the circle represents the two states of the flip-flops and the arcs with arrow heads indicate the state transitions for specific inputs of the flip-flop. For example, when SR flip-flop is in state 0, it goes to state 1 if SR inputs are 10, i.e. S = 1 and R = 0.

3. Flip-Flop Excitation Table

• During the design process we know, from the transition table, the sequence of states, i.e., the transition from each present state to its corresponding next state. From this information we wish to find the flip-flop input conditions that will cause the required transition. For this reason, we need a table that lists the required inputs for a given change of state. Such a table is known as an excitation table of the flip-flop. 

• We can derive the excitation tables for flip-flops from their truth tables. The excitation table consists of two columns Q_n and Q_n+1, and a column for each input to show how the required transition can be achieved. Let us see the truth tables and excitation tables for RS, JK, D and T flip-flops.

a. SR Flip-Flop

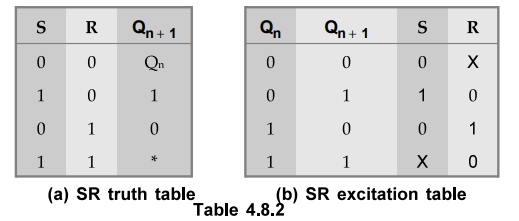
• Table 4.8.2 (a) and (b) show the truth table and excitation tables for SR flip-flop, respectively. As shown in the table, there are four possible transitions from the present state to the next state. For each transition, the required input condition is derived from the information available in the truth table. Let us see the process by examining each case.

Note : The symbol "X" in the table represents a don't care condition, i.e., it indicates that to get required output it does not matter whether the input is either 1 or 0.

0 → 0 Transition : The present state of the flip-flop is 0 and is to remain 0 when a clock pulse is applied. Looking at truth table of SR flip-flop we can understand that, this can happen either when R = S = 0 (no-change condition) or when R = 1 and S = 0. Thus, S has to be at 0, but R can be at either level. The table indicates this with a "0" under S and an "X" (don't care) under R.

0 → 1 Transition : The present state is 0 and is to change to 1. This can happen only when S = 1 and R = 0 (set condition). Therefore, S has to be 1 and R has to be 0 for this transition to occur.

1 → 0 Transition : The present state is 1 and is to change to a 0. This can happen only when S = 0 andR = 1 (reset condition). Therefore, S has to be 0 and R has to be 1 for this transition to occur.

1 → 1 Transition : The present state is 1 and is to remain 1. This can happen either when S = 1 and R = 0 (set condition) or when S = 0 and R = 0 (no change condition). Thus R has to be 0, but S can be at either level. The table indicates this with a "X" under S and "0" under R.

b. JK Flip-Flop

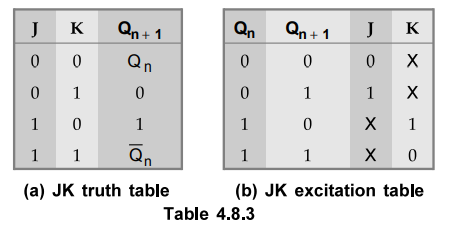
• The truth table and excitation table for JK flip-flop are shown in Table 4.8.3 (a) and (b) respectively. Let us examine each case.

0 → 0 Transition : When both present state and next state are 0, the J input must remain at 0 and the K input can be either 0 and 1.

0 → 1 Transition : The present state is 0 and is to change to 1. This can happen either when J = 1 and K = 0 (set condition) or when J = K = 1 (toggle condition). Thus, J has to be 1, but K can be at either level for this transition to occur.

1 → 0 Transition : The present state is 1 and is to change to 0. This can happen either when J = 0 and K = 1 or when J = K = 1. Thus, K has to be 1 but J can be at either level.

1 → 1 Transition : When both present state and next are 1, the K input must remain at 0 while the J input can be 0 or 1.

• As seen from Table 4.8.3, the excitation table for JK flip-flop has more don't care conditions than the excitation table for RS flip-flop. The don't care terms usually simplify the function. Therefore, the combinational circuits using JK flip-flops for the input functions are likely to be simpler than those using RS flip-flops.

c. D Flip-Flop

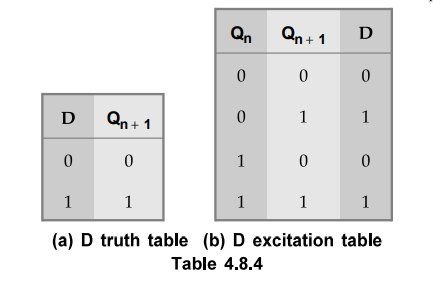
• The Table 4.8.4 (a) and (b) show the truth table and excitation table for D flip-flop, respectively. In D flip-flop, the next state is always equal to the D input and it is independent of the present state. Therefore, D must be 0 if Q_{n +1} has to be 0, and 1 if Q_{n + 1} has to be 1, regardless of the value of Q_n.

d. T Flip-Flop

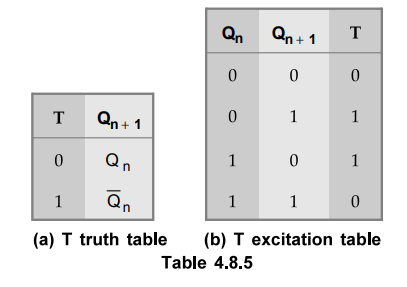
The Table 4.8.5 (a) and (b) show the truth table and the excitation table for T flip-flop, respectively. We know that when input T = 1, the state of the flip-flop is complemented; when T = 0, the state of the flip-flop remains unchanged. Therefore, for 0 →     0 and 1→ 1 and 1 → 0 transitions T must be 1.

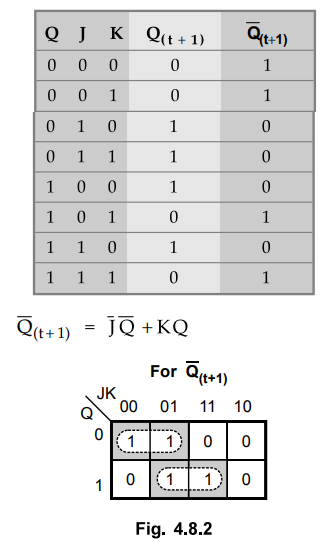
Ex. 4.8.1 Show that the characteristic equation of Q'_(t+l) of JK flip-flop is Q_(t+l) = j Q + KQ

AU : Dec.-07, Marks 4

Sol.: From Fig. 4.8.2 we can write truth table for JK flip flop as shown below.

Review Questions

1. State the characteristics equations of various flip-flops.

2. Give the characteristic equation and state diagram of JK flip-flop.

AU : May-10, Marks 2

3. Sketch the state diagram of D flip-flop.

AU : Dec.-12, Marks 2

4. Draw state diagram of SR flip-flop.

5. Give the state diagram of JK flip-flop.

AU : Dec.-l0, 15, Marks 2

AU : May-07,10, Dec.-12, Marks 2

6. Give the state diagram of various flip-flops.

7. Give the excitation table of SR flip-flop.

AU : Dec.-03, Marks 2

8. Give the excitation table for JK flip-flop.

9. Obtain the excitation table of D flip-flop.

10. Obtain the excitation table for T flip-flop.