Statistics and Numerical Methods: Unit V: Numerical Solution of Ordinary Differential Equations
Adams-bash forth predictor and corrector methods
Solved Example Problems
Milne's method is simple and has a good local error, O(h). However, it is subjected to instability in certain cases the errors do not tend to zero as h is made smaller.
ADAMS-BASH FORTH PREDICTOR AND CORRECTOR METHODS
Milne's
method is simple and has a good local error, O(h). However, it is subjected to
instability in certain cases the errors do not tend to zero as h is made
smaller. Because of this instability, another method, a modification of Adam's
method, is more widely used than Milne's. The Adam's method is a method that
does not have the same instability problem as the Milne's method, but is
efficient. We have stressed that the advantage of the Adam's method over that
of Milne's is that it is stable rather than unstable like Milne's method. An
analytical proof of the stability of Adam's method by examining a particular
equation is not entirely satisfying because we cannot prove its stability for
all cases in that way.
Predictor
formula is
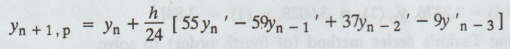
Corrector
formula is
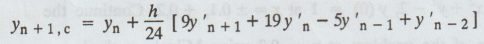
1.
Given dy/dx = x2 (1+ y), y(1) = 1, y (1.1) = 1.233, y (1.2) = 1.548,
y (1.3) = 1.979, evaluate y (1.4) by
Adams-Bashforth method. [A.U. N/D 2004, A.U M/J 2012, Trichy N/D 2010, Tvli,
N/D 2011] [A.U A/M 2015 (R8-10)]
Solution
:
2.
Find y (0.1), y (0.2), y (0.3) from dy / dx = xy + y2, y (0) = 1 by
using Runge-Kutta method and hence obtain y (0.4) using Adam's method.
[A.U
A/M 2010]
Solution
:
3.
Using Adams-Bashforth method, find y (4.4) given 5xy' + y2 = 2 y (4)
= 1, y (4.1) = 1.0049, y (4.2)=1.0097 and y (4.3) = 1.0143. [A.U M/J 2014] [A.U
M/J 2016 (R8-10)]
Solution:
4.
Find y (0.1), y (0.2) and y (0.3) using R-K method of fourth order given dy /
dx (1 + x) y2, y(0) = 1.
Continue
your calculations to find y (0.4), using Adam's method.
Solution
:
5.
Using the above predictor-corrector equations, evaluate y(1.4), if y satisfies.
dy/dx
+ y /x = 1/x2 ⇒
dy /dx = 1 / x2 – y/x = 1 – xy/x2
and y(1) = 1, y(1.1) = 0.996, y(1.2) = 0.986, y(1.3) = 0.972.
[A.U.
N/D 2006] [A.U N/D 2020 R-17] [A.U A/M 2021 R-17]
Solution:
In
the usual notation, we have
Statistics and Numerical Methods: Unit V: Numerical Solution of Ordinary Differential Equations : Tag: : Solved Example Problems - Adams-bash forth predictor and corrector methods
Statistics and Numerical Methods: Unit V: Numerical Solution of Ordinary Differential Equations
Under Subject
Statistics and Numerical Methods
MA3251 2nd Semester 2021 Regulation M2 Engineering Mathematics 2 | 2nd Semester Common to all Dept 2021 Regulation
Related Subjects
Professional English II
HS3251 2nd Semester 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Statistics and Numerical Methods
MA3251 2nd Semester 2021 Regulation M2 Engineering Mathematics 2 | 2nd Semester Common to all Dept 2021 Regulation
Engineering Graphics
GE3251 eg 2nd semester | 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Physics for Electrical Engineering
PH3202 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Basic Civil and Mechanical Engineering
BE3255 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Physics for Electronics Engineering
PH3254 - Physics II - 2nd Semester - ECE Department - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Electrical and Instrumentation Engineering
BE3254 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Circuit Analysis
EC3251 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Materials Science
PH3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Physics for Civil Engineering
PH3201 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Basic Electrical, Electronics and Instrumentation Engineering
BE3252 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Physics for Information Science
PH3256 2nd Semester CSE Dept | 2021 Regulation | 2nd Semester CSE Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation
Programming in C
CS3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation