Euler and Modified Euler Method

EULER AND MODIFIED EULER METHOD

The Taylor's series method may be difficult to apply if the derivatives become complicated and in this case the error is difficult to determine.

The error in a Taylor's series will be small if the step size h is small. In fact, if we make h small enough, we need a few terms of the Taylor's series expansion for good accuracy. The Euler method follows this idea to the extreme. For first order differential equations it uses only the first two terms of the Taylor series. It is one of the oldest methods, suppose, we have to find successively y₁, y₂, ... y_m' where y_m is the value of y corresponding to x = x_m where x_m = x₀ + mh, m 1, 2, ... h being small.

In this method, we use the property that in a small interval a curve is nearly a straight line. Thus, at the point (xo, yo), we approximate the curve by the tangent at the point (x₀, y₀).

The equation of the tangent at (x₀, y₀) is

Hence, the value of y corresponding to x = x₁ is given by

У₁ – y₀ = (dy/dx)_{(x0, y0)} f (x₀,y₀)

У₁  = y₀ + h f (x₀,y₀) … (1)

(1) gives the approximate value of y₁

Similarly, approximating the curve in the next interval (x₁, y₁) by a line through (x₁,y₁) with slope f (x₁, y₁), we get

y₂ = y₁ + hf (x₁,y₁)

In general it can be shown that

y_n+1 = y_n + hf (x_n, y_n), n = 0, 1, 2, ...

This formula is called Euler's algorithm.

Thus in Euler's method the actual curve of solution is approximated by a sequence of line segments. It can happen that the sequence of lines deviates from the curve of solution significantly.

Modified Euler's method

Let P₀ (x₀, y₀) be the point on the solution curve.

Let P₀ A be the tangent at (x₀, y₀) to the curve. Now let this tangent

Now, draw the line through P (x₀, y₀) with this slope. Let this line meet

x = x₁ at K₁ (x₁, y₁⁽¹⁾)^. This y₁⁽¹⁾)^. is taken as the approximate value of y at x = x₁..

1. Using Euler's method find y (0.2), y (0.4) and y (0.6) from dy/dx = x + y, y (0) = 1 with h = 0.2. [A.U M/J 2000, N/D 2007, A/M 2010, A/M 2011, M/J 2012, A.U. Tvli M/J 2010, CBT N/D 2010]  [A.U A/M 2015 R-8] [A.U N/D 2021 R-17]

Solution:

2. Using Euler's method, solve y' = x+y+ xy, y (0) = 1 compute y at [Tx = 0.1, by taking h= 0.05.

 Solution:

Given: f(x, y) = x + y + xy, x₀ = 0, y₀ = 1, h = 0.05,

3. Using Euler's method, find y (0.3) of y (x) satisfies the initial value problem, dy / dx = 1/2 (x² + 1) y2, y (0.2) = 1.1114 [A.U. Nov. 1996]

Solution :

4. Using Euler's method find the solution of the initial value problem dy / dx = log (x + y), y(0) = 2 at x = 0.2 by assuming h = 0.2. [Anna, March 1996] [A.U M/J 2012]

Solution:

5. Compute y at x = 0.25 by modified Euler's method given y' = 2xy, reepy (0) = 1. [A.U CBT A/M 2011] [A.U. N/D 2021 R-17]

Solution:

6. Using modified Euler's method, compute y (0.1) with h = 0.1 from y = y – (2x/y) y (0) = 1

Solution:

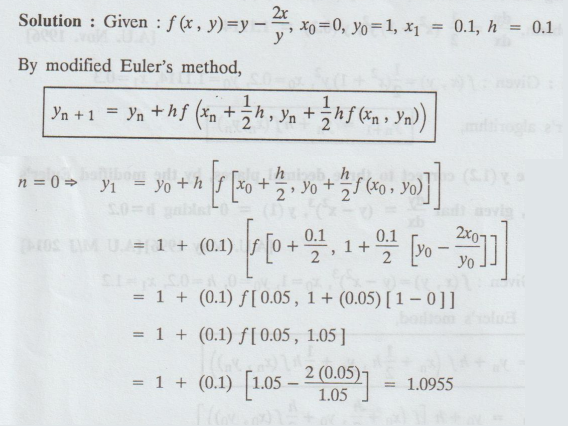
7. Using modified Euler's method, find y (0.1), y (0.2) given that y' = y + e^x with y (0) = 0  [A.U. N/D 2019, R-17]

Solution:

8. Evaluate y (1.2) correct to three decimal places, by the modified Euler's method, given that dy/dx  = (y - x²)³, y (1) = 0 taking b = 0.2

 [A.U. May 1996] [A.U M/J 2014]

Solution :

Given: f(x, y) = (v – x²) ³, x₀ = 1, y₀ = 0, h = 0.2, x₁ = 1.2

By modified Euler's method,

9. Solve y' = 1-y, y (0) = 0 by modified Euler's method. Find y (0.1), y (0.2) and y(0.3).  [A.U. April, 2005] [A.U CBT A/M 2011]

Solution :

10. Using modified Euler's method, find y (0.1) if dy/dx = x² + y², y(0) = 1.

 [A.U. N/D 2004] [A.U N/D 2020 R-17 (NM), A/M 2021 R-17 (NM)]

Solution :

Given: f(x, y) = x²+ y², x₀ = 0, y₀ = 1, h = 0.1, x₁ = 0.1

By modified Euler's method,

11. Consider the initial value problem dy / dx = y - x² + 1, y(0) = 0.5 using the modified Euler's method, find y (0.2) [A.U. A/M 2003] [A.U N/D 2013, N/D 2014] [A.U M/J 2012]

Solution :