Electric Circuit Analysis: Unit I: a. Introduction
Final value theorem
Statement, Formula
If f(t) and its derivative f'(t) are Laplace transformable, then the final value f(oo) of the function f(t) is given by
FINAL
VALUE THEOREM
Statement:
If
f(t) and its derivative f'(t) are Laplace transformable, then the final value
f(oo) of the function f(t) is given by
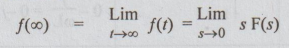
Table 4
To find Z(s) and Y(s) for R, L and
C.
ENERGY SOURCES
Sources
of electrical energy are active elements. These are classified into two types.
They are (i) Voltage source and (ii) Current source.
In
each of the above two, there are again two types namely ideal and non-ideal
(Practical)
1.Voltage
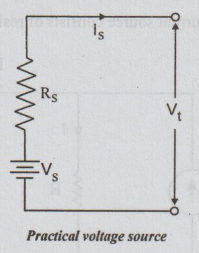
sources: A practical voltage source consists of internal resistance
(source resistance) Rs in series with the source voltage VS.
The terminal voltage Vt across the load changes with change in the
load current. It is due to the voltage drop across RS.
Vt
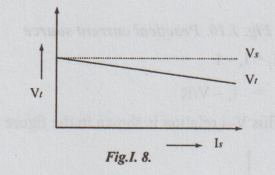
= Vs - Is Rs
As
I increases, Vt decreases. This relation between Is and Vt
is shown graphically as below.
Ideal
Voltage Source:
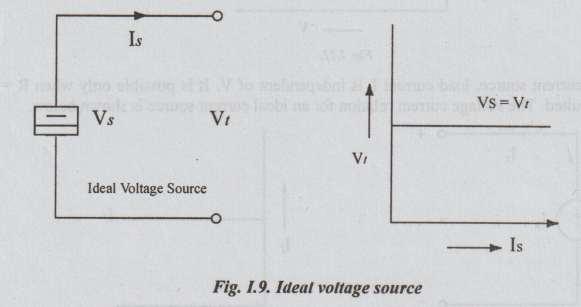
Here
the terminal voltage Vt is independent of current. It is possible
only when RS= 0. Hence the internal resistance of an ideal voltage
source is Zero. The symbol for such a source and the terminal voltage - current
relations of such cases are shown below.
hobi
ne to VS = Vt bioto-nago el
2.
Current source: A practical current source consists of
resistance is parallel with the source.
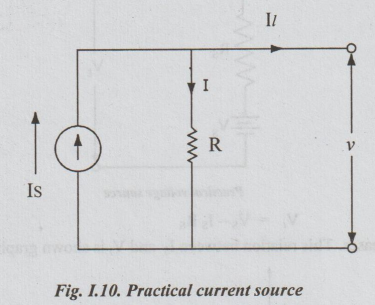
Il
= IS-I
=
IS - V/R
As
V increases, Il decreases. This V-i relation is shown in the figure
below.
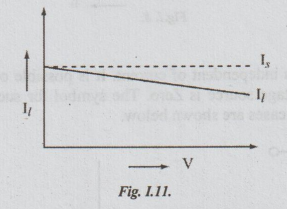
For
an ideal current source, load current Il is independent of V. It is
possible only when R = ∞, i.e., R is open-circuited. The voltage current
relation for an ideal current source is shown below.
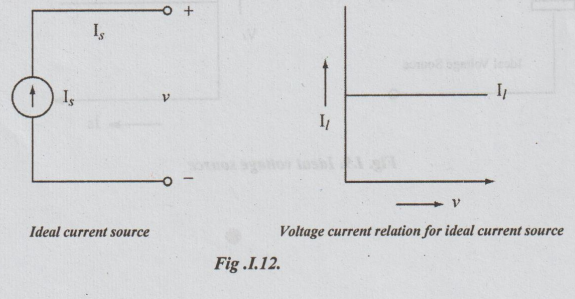
Electric Circuit Analysis: Unit I: a. Introduction : Tag: : Statement, Formula - Final value theorem
Electric Circuit Analysis: Unit I: a. Introduction
Under Subject
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Related Subjects
Professional English II
HS3251 2nd Semester 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Statistics and Numerical Methods
MA3251 2nd Semester 2021 Regulation M2 Engineering Mathematics 2 | 2nd Semester Common to all Dept 2021 Regulation
Engineering Graphics
GE3251 eg 2nd semester | 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Physics for Electrical Engineering
PH3202 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Basic Civil and Mechanical Engineering
BE3255 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Physics for Electronics Engineering
PH3254 - Physics II - 2nd Semester - ECE Department - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Electrical and Instrumentation Engineering
BE3254 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Circuit Analysis
EC3251 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Materials Science
PH3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Physics for Civil Engineering
PH3201 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Basic Electrical, Electronics and Instrumentation Engineering
BE3252 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Physics for Information Science
PH3256 2nd Semester CSE Dept | 2021 Regulation | 2nd Semester CSE Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation
Programming in C
CS3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation