Fourth order runge-kutta method for solving first order equations

FOURTH ORDER RUNGE-KUTTA METHOD FOR SOLVING FIRST ORDER EQUATIONS

The Taylor's series method of solving differential equations numerically is restricted by the work involved in finding the higher order derivatives. However, there are class methods known as Runge-Kutta methods which do not require the calculations of higher order derivatives and give greater accuracy.

These methods have the following useful properties :

1. To evaluate ym+1, they need only information at the point (x_m, y_m).

2. They don't involve the derivatives of f (x, y), such as in Taylor's series method.

3. They agree with the Taylor's series solution upto the terms of h^r, where r differs from method to method and is known as the order of that Range-Kutta method.

Since, Euler's method and modified forms satisfy all the three properties, they can be termed as Runge-Kutta methods of first and second order respectively.

In these methods, the accuracy increases at the cost of calculations. Of this family of methods, the most widely used method is Runge-Kutta of fourth order and so the name Runge-Kutta is used generally for this method. This method coincides with the Taylor's series solution upto terms of h⁴.

1. SECOND ORDER R-K METHOD

If the initial values of (x, y) for the differential equationdy/dx = f(x, y) then the first increment in y namely Ay is calculated from the formula.

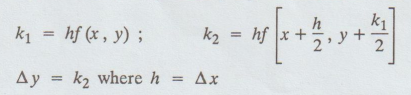
2.  THIRD ORDER R-K METHOD

The algorithm for this method is given below:

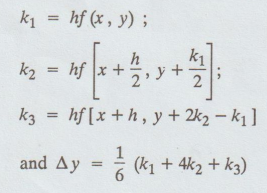
3.  FOURTH ORDER R-K METHOD

The algorithm for this method is given below :

Now, starting from (x1, y1) and repeat the process.

Note 1: The Runge-Kutta method of second order is nothing but the modified Euler method.

Note 2: One of the advantages of these methods is that the operation is identical whether the differential equation is linear or non-linear.

1. Use Runge-Kutta method of the fourth order to find y (0.2) and y (0.4) given that y(dy/dx) = y² – x, y(0) – 2 by taking h= 0.2 (upto four decimal places)

Solution:

2. Given dy/dx = x³ + y, y (0) = 2. Compute y (0.2), y (0.4) and y (0.6) by Runge-Kutta method of fourth order. [A.U. A/M 2004]

Solution:

3. Using R-K method of fourth order, solve dy/dx = y² – x² / y² + x²  with y (0) = 1 at x = 0.2.

[A.U. N/D 2004, 2006, 2007, 2015 (R-13), 2017 (R-8)]

[A.U A/M 2005, 2010, 2015(R-8), 2013, 2017 (R-8)]

Solution:

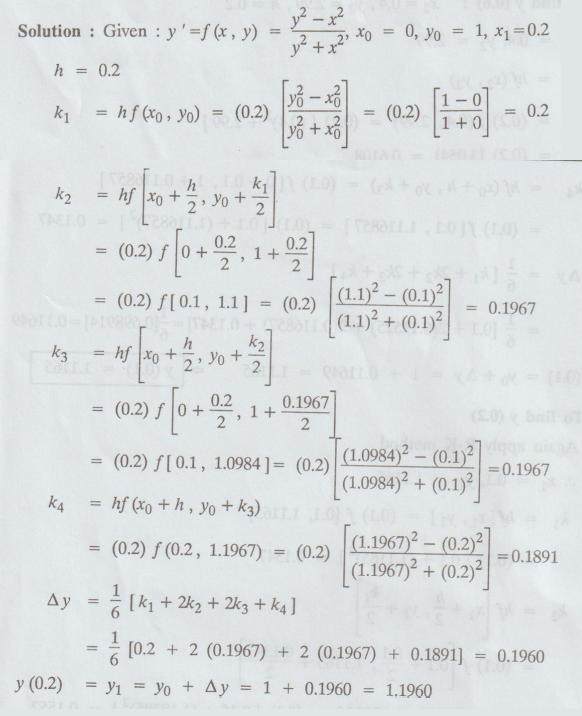
4. Using R-K method of fourth order find y (0.1) and y (0.2) for the initial value problem dy / dx = x + y², y(0)=1. [Anna, Oct. 1996] [A.U N/D 2010] [A.U N/D 2017 R-13]

Solution:

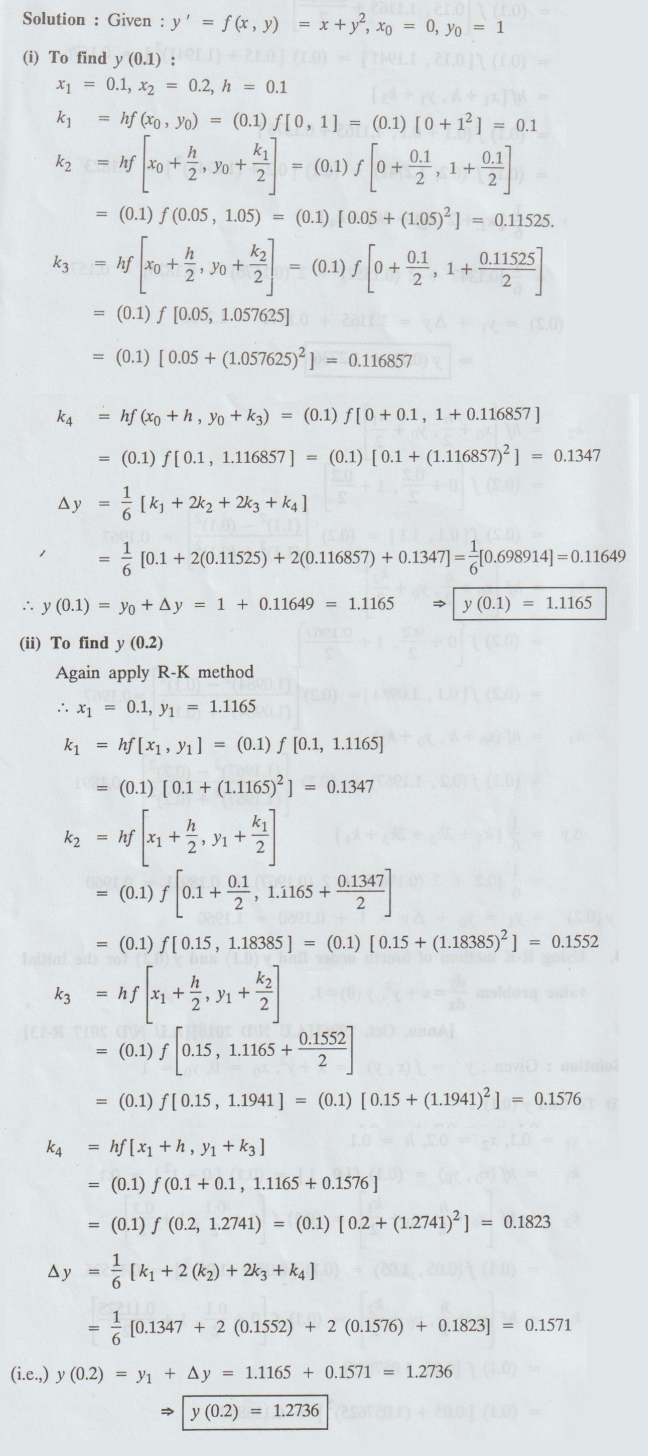
5. Use the fourth order R-K method to compute y for x = 0.1, given y' = xy / 1 + x², y(0) = 1, take h= 0.1.

Solution:

6. Find y (0.7) & y (0.8) given that y' = y − x², y (0.6) = 1.7379 by using Runge-Kutta method of fourth order. Take h = 0.1.

[Anna, April, 2000] [A.U M/J 2012] [A.U N/D 2016 R-13]

Solution:

7. Apply fourth order Runge-Kutta method to determine y (0.1) and  y (0.2) with h = 0.1 from dy/dx = x² + y², y(0) = 1.

[A.U. May 2000, CBT M/J 2010, A/M 2011] [A.U N/D 2019 R17]

Solution: