Grouping of capacitors

GROUPING OF CAPACITORS

The capacitors of different capacitances rated vat different voltages are available in the market. To obtain the required value, the capacitors may be connected in parallel (for large value), in series (for smaller value) or in series - parallel grouping.

Case 1: Capacitors in series

Let C₁and C₂ be two linear time variant capacitors in series as shown in the fig. The applied voltage will be equal to the sum of the voltages across C₁ and C₂, according to KVL.

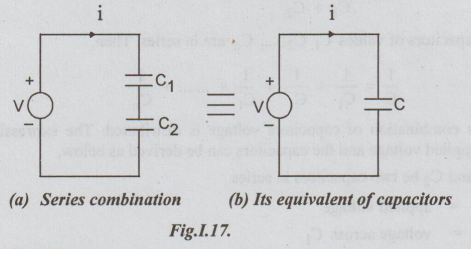
Note: By definition of capacitance,

q = Cv

But, i = dq /dt = C dv/dt

V = 1/C [ i dt]

After cancelling ∫ i dt on both sides, we get

1/C =1/C₁ +1/C₂

C = C₁C₂ / C₁+C₂

Note: If 'n' capacitors of values C₁, C₂, .... C_n are in series. Then,

1/C = 1/C₁ +1/C₁ + 1/C₁+ .....+1/C_n

In series combination of capacitors voltage is distributed. The expression for the voltages, in terms of the applied voltage and the capacitors can be derived as below.

Let C₁ and C₂ be two capacitors in series

V = applied voltage

V₁= voltage across C₁

V₂ = voltage across C₂

Q = Charge across C₁ as well as C₂ (for a series combination charge across each capacitor is same)

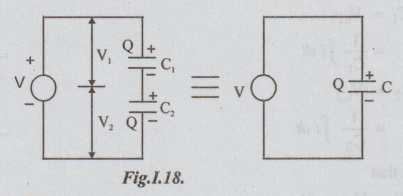
Charge Q = CV

From series combination, Charge is the same

i,e.,

Q = C₁ V₁ = C₂ V₂..... (a)

V₂ = V₁ V₂ / C₂ .... (b)

But  V₁+V₂ = V ....(c)

Substituting (b) in (c), we get

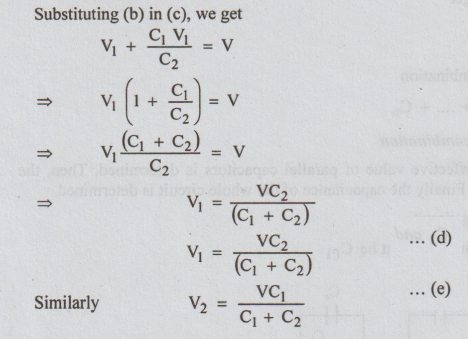
Case 2: Capacitors in parallel

Consider two capacitors having capacitors C₁ and C₂ in parallel as shown in the fig. Assume that all the initial conditions in the capacitors are zero.

In the parallel combination, voltage across each capacitor will be same.

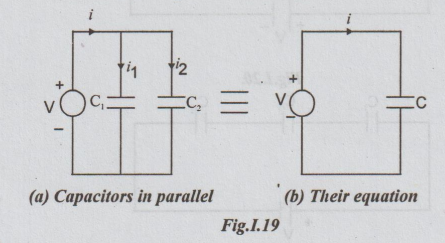
We know that,

i = 1_i + i₂ ............(a)

But i = C dv / dt , i₁ = C₁ dv /dt

And i = C₂ dv / dt

Substituting these values in (a), we get,

C dv/dt = C₁ dv / dt + C₂ dv /dt

⇒ c dv/dt = (C₁ + C₂) dv / dt

After cancelling dv / dt on both sides, we get

C = C₁+ C₂

Note: Capacitors in series - parallel combination

C = C₁+ C₂+ C₃ + ... + C_n

Case 3: Capacitors in series - parallel combination

In this type of circuits, first the effective value of parallel capacitors is determined. Then, the circuit is reduced to series combination. Finally the capacitance of the whole circuit is determined.

As example, consider the following circuit.

C₂ and C₃ are in parallel. Let their equivalent be C_pl

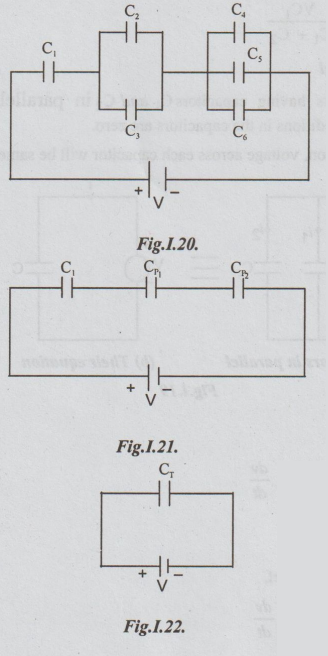
Then, C_PI = C₂+ C₃

C₄, C₅, C₆ are in parallel. Let their equivalent be C_p2

Then, C_p2 = C₄+ C₅+ C₆

Now C₁,C_p1 and C_p2 are in series. Let the equivalent capacitance be C_T

1 / C_T = 1/C₁ + 1/ C_P1 + 1/C_P3

From the above equation we can calculate C_T

Note: If another capacitor of capacitance C₇ is connected across the supply in the given figure, then, finally we will get two capacitance in parallel. Then, the equivalent capacitance will be their sum.