Electric Circuit Analysis: Unit I: a. Introduction
Grouping of inductors
in series and parallel
Inductors can be connected either in series or parallel or combination of both. Here it is assumed that the inductors are connected electrically and isolated magnetically i.e., there is no magnetic coupling between the elements.
GROUPING
OF INDUCTORS
Inductors
can be connected either in series or parallel or combination of both. Here it
is assumed that the inductors are connected electrically and isolated
magnetically i.e., there is no magnetic coupling between the elements.
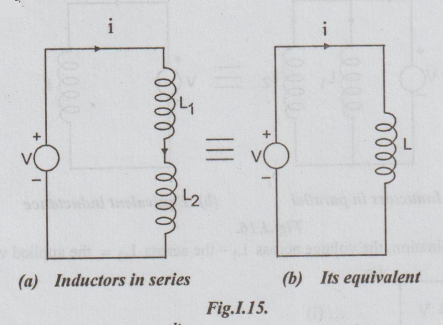
Case 1: Introductions in series
Let
L1 and L2 be the two linear time variant inductors in
series. Let V be the voltage applied and be the current flowing.
The
self induced emf in L1 = e1 = -L1 dt / di
The
self induced emf in = L2 = e2 = -L2 di / dt
The
total self induced emf = e1 + e2
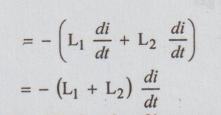
According
to Lenz's law, this self induced emf is to oppose the applied voltage i,e.,
-
(L1 + L2) di / dt = –V
⇒ (L1+L2)di/dt =
– V....(i)
If
L be the equivalent of the above series combination, the induced emf in it
=
–L di / dt
Therefore,
L di/dt = V .....(ii)
From
equation (i) and (ii) we write that
L
di/dt = (L1 + L2) di/dt
L
= (L1 + L2)
Thus,
the inductors in series can be added to obtain the equivalent single inductor.
Case 2: Inductors in parallel
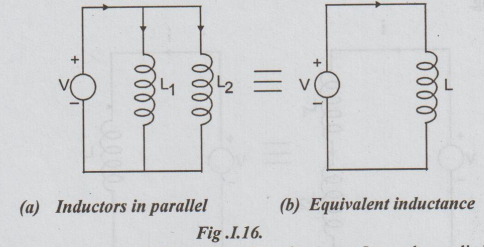
From
the parallel combination, the voltage across L1 = the across L2
= the applied voltage.
i,e.
L1
di1 / dt = L2 di2/dt = V ... (i)
di1/dt
= V/L1 and di2/dt = V/ L2 ......(ii)
But
by KCL, i = i1 + i2 ...(iii)
Differentiating
on both sides of equation (iii), we get
Note:
If 'n' inductors are in parallel,
1/L
=1/L1 +1/L2 +1/L3+.....1/Ln
Electric Circuit Analysis: Unit I: a. Introduction : Tag: : in series and parallel - Grouping of inductors
Electric Circuit Analysis: Unit I: a. Introduction
Under Subject
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Related Subjects
Professional English II
HS3251 2nd Semester 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Statistics and Numerical Methods
MA3251 2nd Semester 2021 Regulation M2 Engineering Mathematics 2 | 2nd Semester Common to all Dept 2021 Regulation
Engineering Graphics
GE3251 eg 2nd semester | 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Physics for Electrical Engineering
PH3202 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Basic Civil and Mechanical Engineering
BE3255 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Physics for Electronics Engineering
PH3254 - Physics II - 2nd Semester - ECE Department - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Electrical and Instrumentation Engineering
BE3254 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Circuit Analysis
EC3251 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Materials Science
PH3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Physics for Civil Engineering
PH3201 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Basic Electrical, Electronics and Instrumentation Engineering
BE3252 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Physics for Information Science
PH3256 2nd Semester CSE Dept | 2021 Regulation | 2nd Semester CSE Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation
Programming in C
CS3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation