Milne's predictor and corrector methods for solving first order equations

MILNE'S PREDICTOR AND CORRECTOR METHODS FOR SOLVING FIRST ORDER EQUATIONS

Runge-Kutta methods are called single-step methods because they use only the information from the last step computed. The methods of Milne's predictor-corrector and Adams-Bashforth predictor corrector formulae are multi-step methods.

In the previous method to calculate the value of yn+1, we need only the information at (x_n, y_n) and we do not care for the nature of the solution. But, the methods of this section remove this objection. As obvious by the name, we first predict the value of y_{n + 1} by some formula, known as "predictor formula" and then recorrect this value by another formula, called "corrector formula". The values are called as predicted and corrected values respectively.

Milne's predictor-corrector formula

Milne's method is the most common multi-step method that first predicts a value for yn+1 from three past values of the derivative. It differs from the Adam's method. In that it integrates over more than one interval. The past values that we require may have been computed by R-K method, or possibly by the Taylor's series method. In the Milne method, we suppose that four equispaced starting values of y are known, at the points

x_n, x_n-1 , x_n-2 and x_n-3

Milne's predictor and corrector formula is

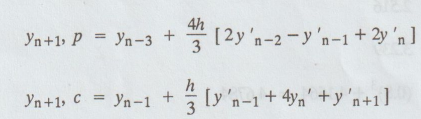
1. Given dy/dx = x³ + y, y(0) = 2. The values of y (0.2) = 2.073, y (0.4) = 2.452, and y (0.6) = 3.023 are got by R-K method of fourth order. Find y (0.8) by Milne's predictor-corrector method taking h = 0.2.  [A.U. A/M 2004, M/J 2014] [A.U N/D 2017 R-13]

Solution: Here,

2. Using Milne's  method find y(4.4) given 5xy + y² – 2 = 0 given y(4) = 1, y (4.1) = 1.0049, y(4.2) = 1.0097 and y (4.3) = 1.0143.

Solution :

3. Solve y' = x - y², 0 ≤ x ≤ 1, y(0) = 0, y (0.2) = 0.02, y (0.4) = 0.0795; y (0.6) = 0.1762 by Milne's method to find y (0.8) and y (1). [A.U. A/M 2005, A.U. Oct. 1996, N/D 2010]

Solution :

4. Using Milne's method find y (2), if y (x) is the solution of dy/dx = 1/2  (x + y) given y (0) = 2, y (0.5) = 2.636, y (1) = 3.595 and y (1.5) = 4.968.

Solution :

5. Determine the value of y (0.4) using Milne's method given y' = xy + y², y (0) = 1; use Taylor series to get the values of y (0.1), y (0.2) and y (0.3). [A.U M/J 2009, A/M 2015 R13, R8]  [A.U A/M 2017 R-13]

Solution:

6. Given y' 1-y and y (0) = 0, find

(i) y (0.1) by Euler's method.

(ii) y (0.2) by modified Euler's method.

(iii) y (0.4) by Milne's method.

Solution :

By Euler’s method,

y₁ = y₀ + hf (x₀ , y₀ ) = 0 + (0.1) (1 - y₀) = 0.1

By modified Euler’s method:

7. Solve: y = x² + y² - 2 using Milne's method for x = 0.3 given

Solution:

We have to calculate y (0.3) by Milne's method.

Milne's predictor formula is

8. Using Runge-Kutta method Calculate y (0.1), y (0.2) and y (0.3) given that dy /dx - 2xy / 1 + x²  = 1, y (0) = 0. Taking these values as starting values  find y (0.4) by Milne's method.

Solution:

9. Using Runge-Kutta method of order 4, find y for x = 0.1, 0.2, 0.3 given that dy/dx = xy + y², y (0) = 1 and also find the solution at x = 0.4 using Milne’s mrthod.

 [A.U. N/D 2003] [A.U M/J 2006, Tvli M/J 2010, N/D 2010, A/M 2011, N/D 2014] L.) ([A.U N/D 2019 R-13]

Solution:

Given: y' = xy + y²

By using R.K. Algorithm.

(i) To find y (0.1): Here x₀ = U, y₀ = 1, h = 0.1

10. Use Milne's predictor-corrector formula to find y (0.4), given

dy/dx  = (1+x²)y² / 2, y (0) = 1, y (0.1) = 1.06, y (0.2) 1.12 and y (0.3) = 1.21

 [A.U A/M 2010, N/D 2011] [A.U. N/D 2020 R-17, A/M 2021 R-17]

Solution :

11. Given y = 1/x+y, y(0) = 2, y (0.2) = 2.0933, y (0.4) = 2.1755, y (0.6) = 2.2493, y (0.8) by Milne's predictor corrector ethod. [AU Tvli M/J 2010] [A.U M/J 2012] [A.U N/D 2021 R-17]

Solution :

12. Given dy/dx  = x² (1 + y) and y(1) = 1, y(1.1) = 1.233, y (1.2) = 1.548, y (1.3)= 1.979, evaluate y (1.4) by using Milne's method. [A.U N/D 2019 (R17)]

Solution :

Given: y' = x² (1+y)  … (1)

Here, h = 0.1