Short Questions and Answers

SHORT QUESTIONS AND ANSWERS

1. State the disadvantage of Taylor's series method. [M.U. Oct.96]

[A.U CBT A/M 2011] [A.U M/J 2012, M/J 2014]

Solution:

In the differential equation dy/dx = f(x, y), the function f(x, y) may have a complicated algebraical structure. Then, the evaluation of higher order derivatives may become tedious. This is the demerit of this method.

2. Write down the fourth order Taylor's Algorithm.

Solution: y_m + 1 = y_m + hy_m’ +  h² / 2! y_m''' + h4 / 4! y^iv_m

Here, yⁿ_m denotes the n^th derivative of y w.r.to x at the point ym (x_m, y_m).

3. Write the merits and demerits of the Taylor method of solution. [M.U. Oct. 96] [A.U N/D 2006, A.U. Tvli N/D 2010]

Solution:

The method gives a straight forward adoptation of classic calculus to develop the solution as an infinite series. It is a powerful single step method, if we are able to find the successive derivatives easily. If f(x, y) involves some complicated algebraic structures, then the calculation of higher derivatives becomes tedious and the method fails. This is the major drawback of this method. However, the method will be very useful for finding the starting values for powerful methods like Runge-Kutta method, Milne's method etc.

4. Which is better Taylor's method or R-K Method? [M.U. Oct. 95]

Solution :

R-K method does not require prior calculation of higher derivatives of y (x), as the Taylor's method does. Since, the differential equations using in applications are often complicated, the calculation of derivatives may be difficult.

Also, the R-K formulas involve the computation of f (x, y) at various positions, instead of derivatives and this function occurs in the given equation.

5. Taylor's series method will be very useful to give some ……. for powerful numerical methods such as Runge-Kutta method, Milne's method etc.

Solution : Initial starting values.

6. State Taylor's series algorithm for the first order differential equation. [A.U N/D 2017 R-8]

Solution :

To find the numerical solution of dy/dx = f(x, y) with the

condition y (x₀) = y₀ We expand y(x) at a general point x_m in a Taylor series, getting y_m + 1= ym + h/y!_m + h2 / 2! y _m’’ + h3 / 3! y _m ‘’’ + …

Here, y^r_m denotes the r th derivatives of y w.r.to x at the point (x_m, y_m).

7. What is the truncation error of Taylor's series method? [A.U. Tvli M/J 2010]

Solution :

8. In solving dy/dx = f(x,y), y (x₀) = y₀, write down Taylor series for y(x₁).

[A.U CBT N/D 2010]

Solution :

9. Write Taylor's formula to solve y' = f (x, y), with y (x₀) = y₀ [A.U. M/J 2007]

Solution:

10. Find y (0.1) if dy/dx = 1+y, y (0) = 1, using Taylor's series method.

Solution:

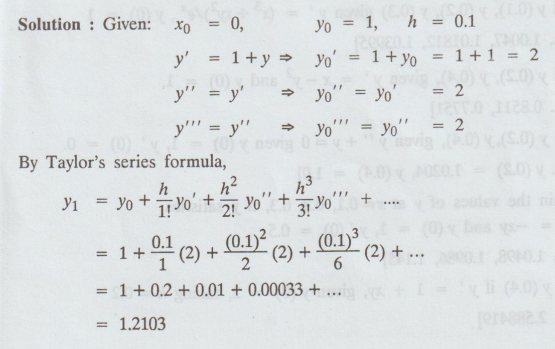
11. What are the various methods of solving ordinary differential equations?

 [A.U A/M 2019 R-17] [A.U N/D 2020 R-17] [A.U A/M 2021 R-17]

Solution :

1. Taylor's series method

2. Euler's method

3. Modified Euler's method

4. R-K method

5. Milne's Predictor Corrector method

6. Adam's Predictor Corrector method