Statistics and Numerical Methods: Unit V: Numerical Solution of Ordinary Differential Equations

Short Questions and Answers

Euler and Modified Euler

Home | Department: EEE Department | Ist Year | Subject: Statistics and Numerical Methods |

Statistics and Numerical Methods : Unit - V : Numerical solution of ordinary differential Equations : Short Questions and Answers

SHORT QUESTIONS AND ANSWERS

1. Write down Euler's algorithm to the differential equation dy/dx = f(x, y). [A.U M/J 2000, N/D 2011, M/J 2013] [A.U N/D 2016 R-13]

Solution :

y_n
+1 = y_n + hf (x_n, y_n) when n = 0, 1, 2,…

This is Euler's algorithm. It can also be written as

y (x + h) = y (x) + hf (x, y)

2. State True or False.

In Euler's method, if h is small, the method is too slow and if h is large, it gives inaccurate value.

Solution :

The statement is true.

3. State modified Euler formula. [A.U A/M 2019 R-13, N/D 2019 R-13]

State modified Euler's algorithm to solve y' = f(x, y), y (x₀) = y₀ at x = x₀ + h. [M.U. Oct. 95, A.U CBT M/J 2010]

[A.U CBT N/D 2011, N/D 2011, M/J 2012] [A.U N/D 2017 R-13]

Solution:

4. Say True or False. The modified Euler method is based on the average of points.

Solution :

The statement is true.

5. Write the truncation error of the Euler's method.

Solution:

6. Write the bound on the truncation error of the Euler's method.

Solution:

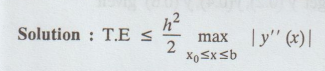
7. State Euler's formula.

Solution :

y_n
+1 = y_n + hf (x_n, y_n) when n = 0, 1, 2, ...

8. Find y (0.2) for the equation y = y + ex, given that y (0) = 0 by using Euler's method.

Solution:

Given: f(x, y) = y + e^x, x₀ = 0, y₀= 0, h = 0.2

By Euler's algorithm,

y₁ = y₀ + hf (x₀, y₀)

= 0 + 0.2f(0, 0) = 0.2 [0+ e⁰] = 0.2

i.e., y (0.2) = 0.2

9. What do you do in improved and modified Euler methods?

Solution :

Improved Euler: We average slopes

Modified Euler: We average points. Euler

10. Using Euler's method, find y at x=0.1, if y' = 1 + xy given that y (0) = 2

[A.U N/D 2019 (R17)] [A.U A/M 2018 (R13)]

Solution :

y' = f(x, y) = 1 + xy

Here, x₀ = 0, y₀= 2, x₁ = 0.1, h = 0.1

Euler's algorithm,

y₁ = y₀ + hf (x₀, y₀) = 2+ (0.1) [1 + x₀y₀]

= 2 + (0.1) [1 +0] = 2 + 0.1 = 2.1

Statistics and Numerical Methods: Unit V: Numerical Solution of Ordinary Differential Equations : Tag: : Euler and Modified Euler - Short Questions and Answers

Home | Department: EEE Department | Ist Year | Subject: Statistics and Numerical Methods |

<< Previous

Next >>

Statistics and Numerical Methods: Unit V: Numerical Solution of Ordinary Differential Equations

Taylor's series method - Solved Example Problems

Taylor's series method for simultaneous first order differential equations - Solved Example Problems

Solving higher order linear differential equations - Taylor's Series Method | Solved Example Problems

Short Questions and Answers - Taylors Series Method

Exercise 5.1 [Taylor's Series Method] - Solved Example Problems

Euler and Modified Euler Method - Solved Example Problems

Short Questions and Answers - Euler and Modified Euler

Exercise 5.2 [Euler and Modified Euler] - Solved Example Problems

Fourth order runge-kutta method for solving first order equations - Solved Example Problems

R-k method for simultaneous first order differential equation - Solved Example Problems

Short Questions and Answers - Fourth order R-K Method

Exercise 5.3 [Fourth order R-K Method] - Solved Example Problems

Milne's predictor and corrector methods for solving first order equations - Solved Example Problems

Short Questions and Answers - Milne's Predictor and Corrector method

Exercise 5.4 [Milne's Predictor and Corrector method] - Solved Example Problems

Under Subject

Statistics and Numerical Methods

MA3251 2nd Semester 2021 Regulation M2 Engineering Mathematics 2 | 2nd Semester Common to all Dept 2021 Regulation

Related Subjects

Professional English II

HS3251 2nd Semester 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation

Statistics and Numerical Methods

MA3251 2nd Semester 2021 Regulation M2 Engineering Mathematics 2 | 2nd Semester Common to all Dept 2021 Regulation

Engineering Graphics

GE3251 eg 2nd semester | 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation

Physics for Electrical Engineering

PH3202 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation

Basic Civil and Mechanical Engineering

BE3255 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation

Electric Circuit Analysis

EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation

Physics for Electronics Engineering

PH3254 - Physics II - 2nd Semester - ECE Department - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation

Electrical and Instrumentation Engineering

BE3254 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation

Circuit Analysis

EC3251 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation

Materials Science

PH3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation

Basic Electrical and Electronics Engineering

BE3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation

Physics for Civil Engineering

PH3201 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation

Basic Electrical, Electronics and Instrumentation Engineering

BE3252 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation

Physics for Information Science

PH3256 2nd Semester CSE Dept | 2021 Regulation | 2nd Semester CSE Dept 2021 Regulation

Basic Electrical and Electronics Engineering

BE3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation

Programming in C

CS3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation