Taylor's series method

UNIT - V

NUMERICAL SOLUTION OF ORDINARY DIFFERENTIAL

EQUATIONS

TAYLOR'S SERIES METHOD

The method gives a straightforward adaptation of classic calculus to develop the solution as an infinite series. It is a powerful single step method, if we are able to find the successive derivatives easily. If f (x, y) involves some complicated algebraic structures, then the calculation of higher derivatives become tedious and the method fails. This is the major drawback of this method. However, the method will be very useful for finding the starting values for powerful methods like Runge-Kutta method, Milne's method etc.

Consider the first order differential equation

dy / dx = f(x, y)   …. (1)

with y (xo) = y₀

Differentiating (1) with respect to x, we get

d²y / dx² = ∂f / ∂x + ∂f / ∂y dy / dx …. (2)

Differentiating this successively, we can obtain y ''', y^iv, ...

putting x = x₀ and y = 0, the values of y₀', y₀'' ... can be obtained.

Hence, the Taylor's series expansion of y (x) at x = xo is given by

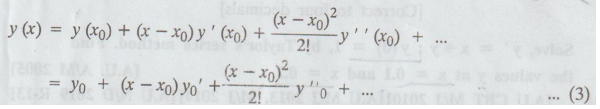
gives the values of y for every value of x for which (3) converges. Let x₁ = x₀ + h and let

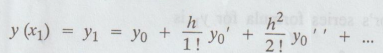
Once y₁ is known, we can compute y₁ , y₁ …. from (1), (2) etc.

Then, y can be expanded in a Taylor's series about x = x₁ and we have

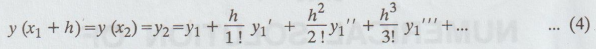
continuing in this way, we find the solution y (x).

 

1. Using Taylor's series method find y at x = 0.1 if dy / dx = x²y - 1,

y (0) = 1.  [A.U. N/D 2004, N/D 2010, N/D 2014 NM]

Solution:

Given y' = x²y - 1 and x₀ = 0, y₀ = 1, h = 0.1

By Taylor's series formula for y₁ is

 

2. Solve, y' = x+y; y (0) = 1, by Taylor's series method. Find the values y at x = 0.1 and x = 0.2.

[A.U. A/M 2005] [A.U CBT M/J 2010]TA.U M/J 2013, M/J 2014] [A.U N/D 2019 R-13]

Solution :

To find y (0.1) : Given y = x + y and x₀ = 0, y₀  = 1 h = 0.1

We know that, the Taylor's series formula for y₁ is

 

3. Solve dy / dx = y² + x² with y (0) = 1. Use Taylor series at x = 0.2 and 0.4. Find x = 0.1

Solution:

Given: y² = y² + x², x₀ = 0, y₀ =1

By Taylor's series formula

 

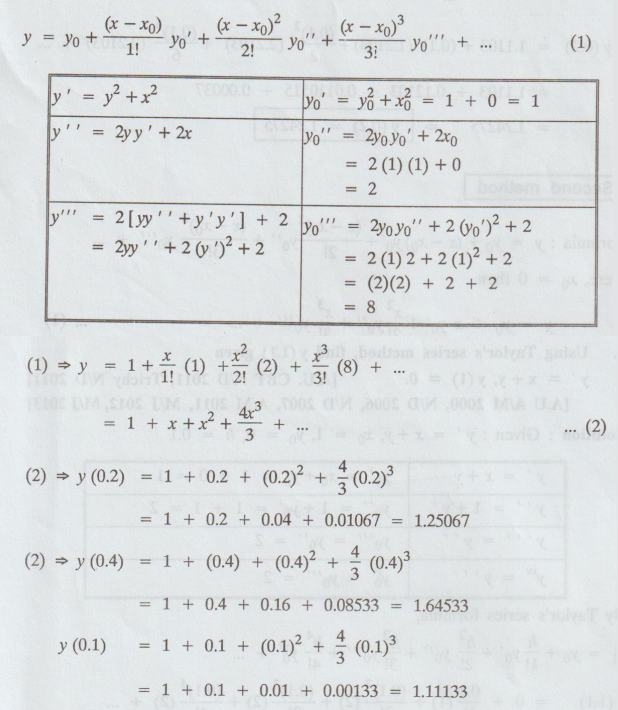
4. Using Taylor's series method find y at x = 0.1 correct to four decimal places from dy / dx = x² - y, y (0) = 1, with h = 0.1. Compute terms upto x⁴

 [A.U. May 2000, Trichy A/M 2010] [A.U M/J 2012] [A.U N/D 2016 R-13] [A.U N/D 2017 R-13]

Solution:

 

5. Using Taylor's series method, find y (1.1) given

y' = x + y, y (1) = 0.

[A.U. CBT N/D 2011, Trichy N/D 2011]

[A.U A/M 2000, N/D 2006, N/D 2007, A/M 2011, M/J 2012, M/J 2013]

Solution:

Given: y = x + y, x₀  = 1, y₀ = 0, h = 0.1

 

6. Find the Taylor's series solution with three terms for the initial value problem. dy/dx = x³ + y, y (1) = 1.

Solution:

 

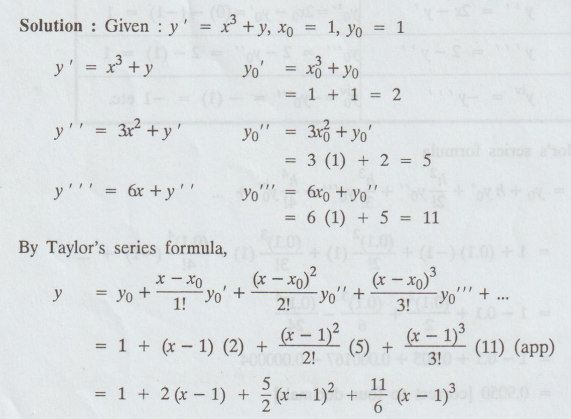
7. Using Taylor's series method with the first five terms in the expansion find y (0.1) correct to three decimal places, given that dy / dx = e^x – y², dy (0) = 1.

 [A.U. May, 1996]

Solution :

 

8. Using Taylor's method, compute y (0.2) and y (0.4) correct to 4 decimal places given dy/dx = 1 - 2xy and y (0) = 0. [A.U N/D 2009, CBT N/D 2010] [A.U A/M 2011]

Solution :

 

9. Apply the Taylor's series method to find the value of y (1.1), y (1.2) and y (1.3) correct to three decimal places given that y' = xy^1/3, y (1) = 1, taking the first three terms of the Taylor's series expansion get the closed form solution of the differential equation and compare the actual values of y to the approximate values calculated. [A.U A/M 2019 R-17]

Solution: Take, x₀ = 1, y₀ = 1, h = 0.1

(i) To find y (1.1):

 

10. By means of Taylor's series expansion, find y at x = 0.1, 0.2 correct to three significant digits given dy / dx - 2y = 3e^x, y (0)=0.

[A.U N/D 2006, A/M 2010, CBT N/D 2011] [A.U N/D 2014] [A.U A/M 2015 R-13] [A.U N/D 2019 R-13] [A.U N/D 2021 (R-17)]

Solution:

Here, x₀ = 0, y₀ = 0, x₁ = 0.1, x₂ = 0.2, h = 0.1

To find y (0.1):

 

11. Using Taylor's method solve dy/dx = 1 + xy with y₀ = 2. Find

(i) y (0.1), (ii) y (0.2) and (iii) y (0.3). [A.U Tvli A/M 2011]

Solution :

 (i) To find y (0.1):

The Taylor's algorithm is

(ii) To find y (0.2):

The Taylor's algorithm for the next approximation is

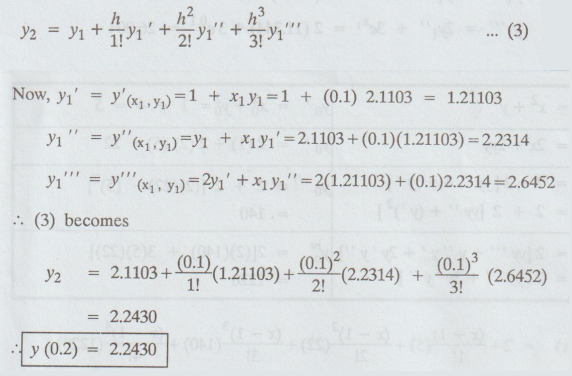
 (iii) To find y (0.3):

The Taylor's algorithm for third approximation is

 

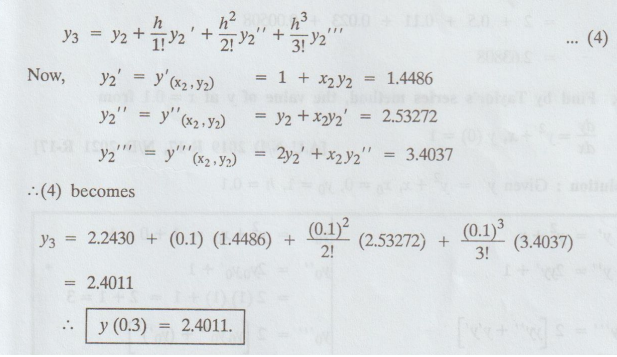
12. Using Taylor's series method, find y at x = 1.1 by solving the equation dy / dx x² + y²; y (1) = 2. Carry out the computations upto fourth order derivative. [A.U M/J 2014 R8 (NM)]

[A.U N/D 2020 R-17, A/M 2021 R-17]

Solution:

y' = x² + y², x₀ = 1, y₀ = 2

By Taylor's series formula

 

13. Find by Taylor's series method, the value of y at x = 0.1 from

dy/dx = y² + x, y (0) = 1

 [A.U N/D 2019 R-17, N/D 2021 R-17]

Solution :

Given y' = y² + x, x₀ = 0, y₀ = 1, h = 0.1