Electric Circuit Analysis: Unit I: a. Introduction
Worked Example Problems
Basic Electric Circuit Analysis
Electric Circuit Analysis: Unit I: Introduction : Worked examples
WORKED EXAMPLES
Example 1: 20 μuF capacitor is changed at a constant current of 5 μA for 10
minutes. Calculate the final p.d across the capacitor and the corresponding
charge in coulombs.
Solution:
Data: C = 20 μF
1
= 5 μA
t
= 10 minutes = 600 sec.
Required: V
and Q
Formula:
Q = It
And
V = Q/C
On
Substitution, we get
Q
= 5 × 10-6 × 600
=
3 × 10-3 coulombs = 3 mc
And
V = 3 × 10-3 / 20 × 10-6
=
150 volts
Example 2: Three capacitors have capacitance of 10 μF, 15 μF and 20 μF
respectively. Calculate the total capacitance when they are connected (a) in
parallel (b) in series.
Solution:
Data: C1 = 10 μF
C2
= 15 μF
С3
= 20 μF
Required:
CT in (a) parallel and (b) series
Formula:
(a)
in parallel СT =C1+ C2+ C3
(b)
in series 1/CT = 1/C1 + 1/C2 + 1/С3
Substituting
the values, we have
(a)
For parallel combination,
CT
= 10× 10-6+ 15 × 10-6 + 20 × 10-6
=
45 × 10-6 F
.CT
= 45 μF
(b)
For series combination,
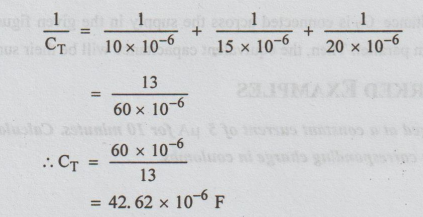
=
42.62 × 10-6 F
CT
= 4.62 μF
Example 3 : Two capacitors, having capacitances of 10 μF and 15 μF respectively,
are connected in series across a 200 v d.c. supply. Calculate: (a) the charge
on each capacitor; (b) the p.d across each capacitor. Also find the capacitance
of a single capacitor that would be equivalent to these two capacitors in
series.
Solution:
Data: C1 = 10 μF
C2
= 15 μF
V
= 200V
Required:
(a)
Q
(b)
V1 and V2
(c)
CT
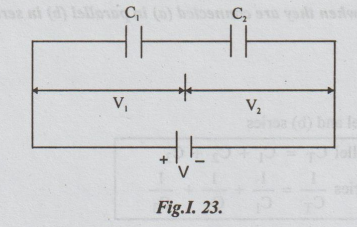
Formula:
For
the series combination
(a)
Q = CTV = C1 V1 = C2 V2
V1
= VC2 / C1+ C2
V2
= VC1 / C1 + C2
(b)
CT = C1 C2 / C1+ C2
Substituting
the given values we get,
(a)
Q = C1 VI
=
10×10-6 × 120 = 1200 μC
(b)
V1 = 200 × 15/25 = 120 volts
V2
= 200 - 120 = 80 volts
(c)
CT = 10 × 15 / 10 +15 6 με
Example 4: A certain capacitor has a capacitance of 3 μF. A capacitance of 2.5 μF
is required by combining this capacitor with another. Calculate the capacitance
of the second capacitor and state how it must be connected to the first.
Solution:
Data: Total capacitance required = 2.5 μF
Capacitance
of capacitor available = C1 = 3 μF
As
the total capacitance is less than the capacitance of the capacitor available,
one more capacitor must be connected in series with C1. Let its
capacitance be C2.
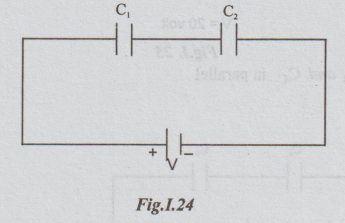
Therefore,
CT
= C1 C2 / C1+ C2
Substituting
known values, we get,
2.5
= 3 × C2 / 3 + C2
⇒ 7.5+ 2.5 C2
= 3 C2
⇒ 0.5 C2 = 7.5
⇒ C2 = 15 μF
in series with C1
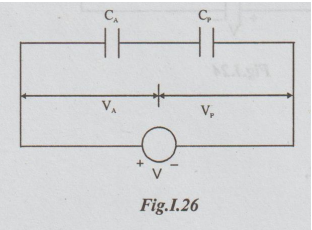
Example 5:
A
capacitor A is connected in series with two capacitors B and C connected in
parallel. If the capacitances of A, B and C are 4,3 and 6 μF respectively,
calculate the equivalent capacitance of the combination. If a p.d of 20v is
maintained across the whole circuit calculate the charge on the 3 μF capacitor.
Solution:
Data:
CA
= 4μF
CB
= 3μF
Cc
= 6 μF
CA
is in series with parallel combination of CB and Cc
V
= p.d across the whole combination
=
20 volts
Required:
(a)
CT
(b)
Charge across B = QB
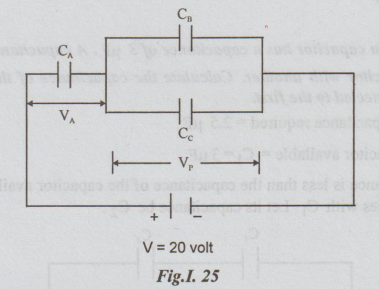
Cp
= equivalent of CB and Cc in parallel
=
CB + CC = 3+6
= 9μF
CT
= equivalent of combination of
CA
and CB in series
=
CA Cp / CA + CP = 4 × 9/13 = 2.77
μF
QB
= CB VB = CB Vp, VB = Vp
By
distribution of voltage formula,
VB
= VCA / CA + CP = 20 × 4 / 4 + 9 = 80/13 = 6.15
volts...(i)
Substituting
the values of CB and Vp in (i)
QB
= 18.45 × 10-6 coulombs
=
18.45 μC
Example 6 :
Given
some capacitors of 0.1 uF capable of withstanding upto 15 v each. Calculate the
number of capacitors needed if it is desired to obtain a capacitance of 0.1 μF
for use in circuit involving 60 V.
Solution:
Data:
Capacitance
of each capacitor = 0.1 μF
Voltage
to which the capacitor can withstand = 15 volts
Total
voltage involved in the circuit = 60 volts
Required:
Total no. of capacitors.
Total
voltage is 60 volts whereas one capacitor can withstand only 15 volts. So there
must be some groups of capacitors. Assume that in each group there are 'n'
capacitors in parallel.
The
equivalent capacitance of each groups = n × 0.1 = 0.1 n μF
The
number of groups in series
=
60 / 15 = 4
Since
there are four such groups in series, the total capacitance
=
CT
=
Capacitance of each group / 4 = 0.1n / 4
Given
that this total capacitance must be equal to 0.1 μF
i.e,
CT = 0.1 μF
(or)
n × 0.1 /4 = 0.1
⇒ n = 4
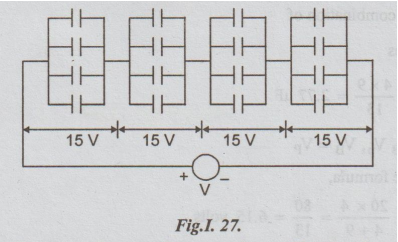
Thus,
in each parallel group there are four capacitors. Like that, there are four
groups. Hence, total number of capacitors required = 4 × 4 = 16.
The
arrangement of capacitors is as shown in the figure.
Example
7: A capacitor having a capacitance of 3 μF is
charged to a potential difference of 200 v and the connected in parallel with
another capacitor of 2 μF capacity. Calculate, assuming no loss of charge, the
voltage across the parallel capacitors.
Solution:
Data:
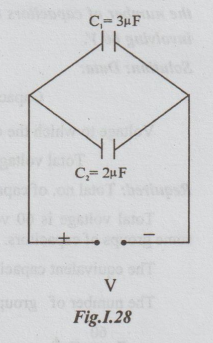
C1
= 3μF
C2 = 2μF
Let
the voltage across the parallel combination be V volts.
Total
charge = Q1 + Q2
=
C1V + C2 V
The
total voltage applied to charge C1, before connecting in parallel
with C2 = 200 volts.
Hence,
Charge across C1 = C1 × 200
=
3 × 10-6 × 200
=
600 × 10 coulomb
As
there is no loss of charge,
C1
V+ C2 V = 600 × 10-6
⇒ V (C1+C2)
= 600 × 10−6
⇒ V = 600 × 10-6 /
C1 + C2 = 600 × 10-6 / 5×10-6
=
120 volts
Electric Circuit Analysis: Unit I: a. Introduction : Tag: : Basic Electric Circuit Analysis - Worked Example Problems
Related Topics
Related Subjects
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
